Ed H
Every year, a team of six pre-university students is selected to represent the United Kingdom at
the prestigious International Mathematical Olympiad, the oldest of the International Science Olympiads. The event is the pinnacle of competitive mathematics for ‘mathletes.’
The national selection process for the team begins with the Senior Mathematical Challenge, run by the United Kingdom Mathematics Trust, or UKMT. This online challenge consists of 25 multiple-choice questions, which gradually increase in difficulty, testing students on difficult and unfamiliar mathematical problems, and their ability to maintain an internet connection for 90 minutes.
The UKMT then selects the top 1,000 or so students for the next stage: the British Mathematical Olympiad’s first round. This is a three-and-a-half-hour paper, consisting of six problems, designed to allow contestants to explore mathematical ideas and find creative strategies to solve them. Around 100 candidates are selected for the second round. Contestants are given the same amount of time to solve just four questions, with the harder ones stretching them to their absolute limits. Then, around 25 high-scoring competitors are invited to a training camp, where the national team of six is selected.
This year, I decided to go all in. I gathered about five pens, stole all the printer paper, and coerced my family into leaving me in peace. Fortunately, this strategy paid off, qualifying me for the first round of the British Olympiad.
Over the next couple of months, I did everything I could to prepare myself, which involved a lot of past papers. I started by averaging around two out of the six questions, but I quickly found myself improving. For each question I could not solve, I would look at the solution and search for the underlying reason why I did not solve it. Often, how a candidate would think of such a solution would be a complete mystery to me, but I started to develop a better intuition for Olympiad-level ideas to the point where I would consistently solve five or six questions on each paper.
By the time the Olympiad came round, I felt properly ready. On the day, I managed to fully solve questions 1-5, which was enough to qualify me for the next round. Interestingly, most of the questions required nothing more than GCSE maths to solve.
Between the first and second rounds, I had another couple of months to prepare for the next stage of selection. I found myself rapidly improving. By the time it was getting close, I was solving about three or four questions per paper.
Unfortunately, on the day of the real round, I only solved Q2 and Q3. The first question involved factorising 7692307 and noticing that it was divisible by 1429. I spent so long on the question that I did not have time for Q4, which was a combinatorics question: my strongest area of Olympiad maths. It was fun to solve after the exam though.
However, I had done just enough to qualify me for the training camp. This will take place in the easter holidays and will finally give me a chance to meet some fellow ‘mathletes.’ I’ll be taught IMO level maths throughout and at the end of it, I will have to complete two four-and-a-half-hour exams, with only 3 questions on each paper! Over the next month or so, I’ll be continuing to learn more Olympiad maths and practicing questions from international competitions, preparing myself for what is to come.
Update:
Following the IMO training camp, I qualified for the British team competing at another premier international mathematical competition: the Balkan Mathematical Olympiad in Varna, Bulgaria. It was an amazing experience, and at the end of it all I scored a bronze medal, which felt incredible!
Solving a Balkan Mathematical Olympiad problem
1 The Problem
Let ABC be an acute triangle such that CA ≠ CB with circumcircle ω and circumcentre O. Let tA and tB be the tangents to ω at A and B respectively, which meet at X. Let Y be the foot of the perpendicular from O onto the line segment CX. The line through C parallel to line AB meets tA at Z. Prove that the line YZ passes through the midpoint of the line segment AC.
Balkan Maths Olympiad 2022, Problem 1
2 Required Olympiad Knowledge
2.1 Isogonal Conjugacy
In any given triangle ABC, the isogonal conjugate of a point P is the intersection of the lines obtained by reflecting AP, BP, CP over the angle bisectors of ∠A, ∠B, ∠C respectively. It is a standard result that these lines are concurrent.
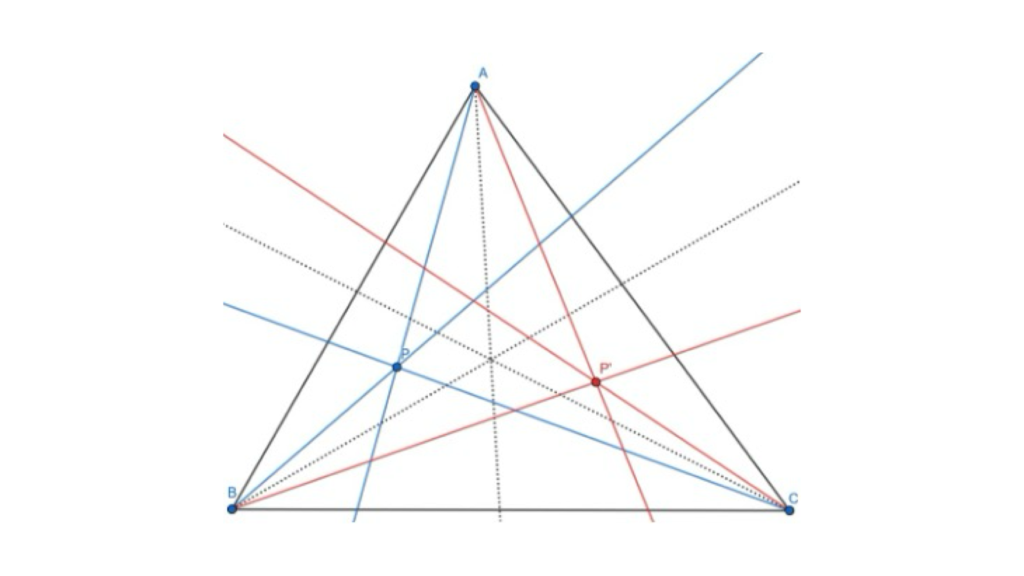
Figure 1: Here, P’ is the isogonal conjugate of P. The dotted lines are the angle bisectors.
2.2 Centroid
In any given triangle ABC, if we let D, E and F be the midpoints of BC, CA, AB respectively, then AD, BE, and CF concur at the centroid. The centroid is one of the standard triangle centres, and can be thought of as the centre of mass of the triangle.
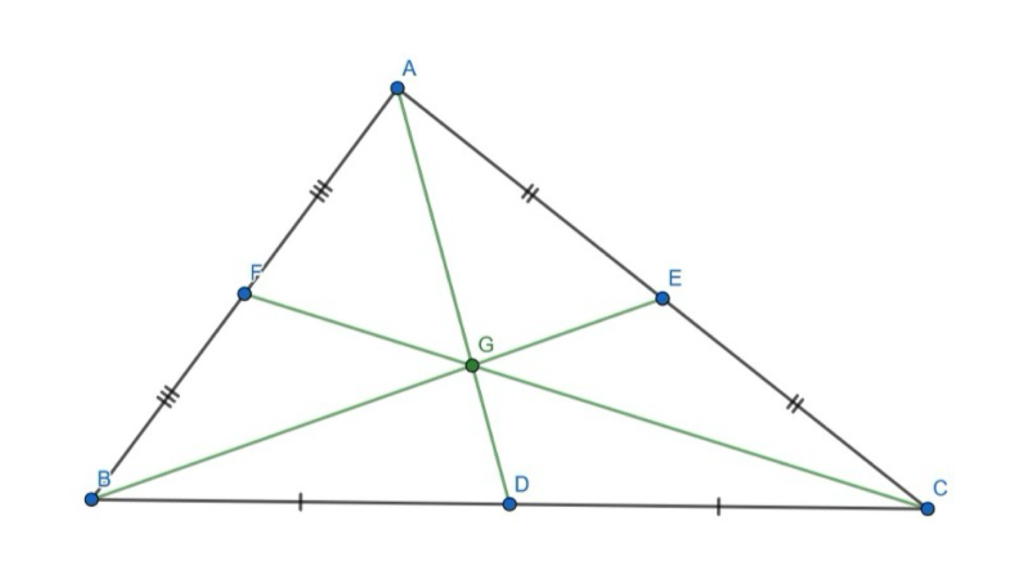
Figure 2: The centroid is often denoted as G.
2.3 Symmedian Point
In any given triangle ABC, with its circumcircle, if we say the tangents at B and C intersect at X, tangents at C and A intersect at Y, and tangents at A and B intersect at Z, then AX, BY, and CZ will concur at the symmedian point. The key fact about the symmedian point is that it is the isotonic conjugate of the centroid.
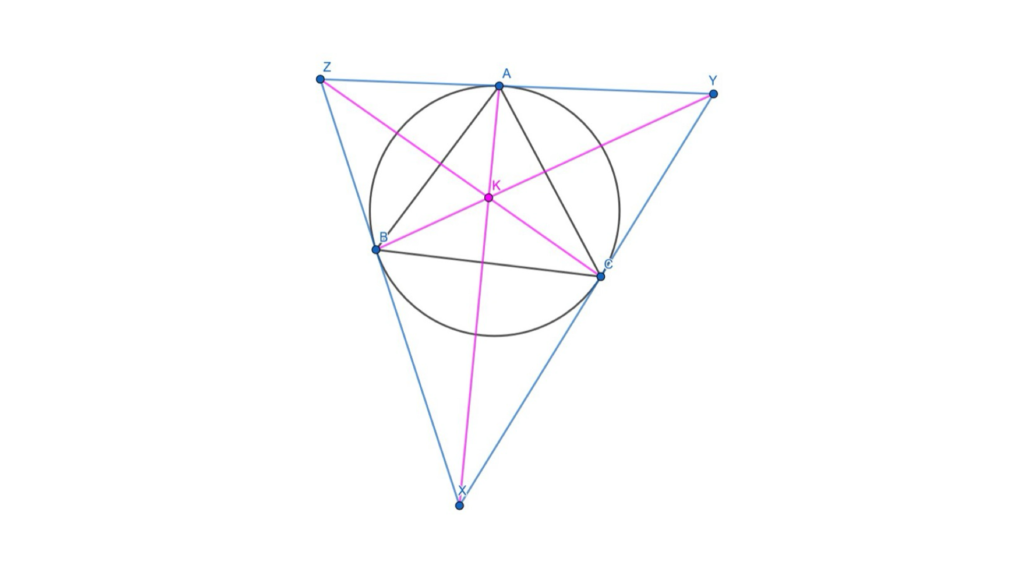
Figure 3: The symmedian point is often denoted as K.
3 My Solution
The only natural way to start is by drawing a large, accurate diagram. My only recommendations for this problem are to draw the circumcircle first, and look at where the compass point marked the paper to find the circumcentre.
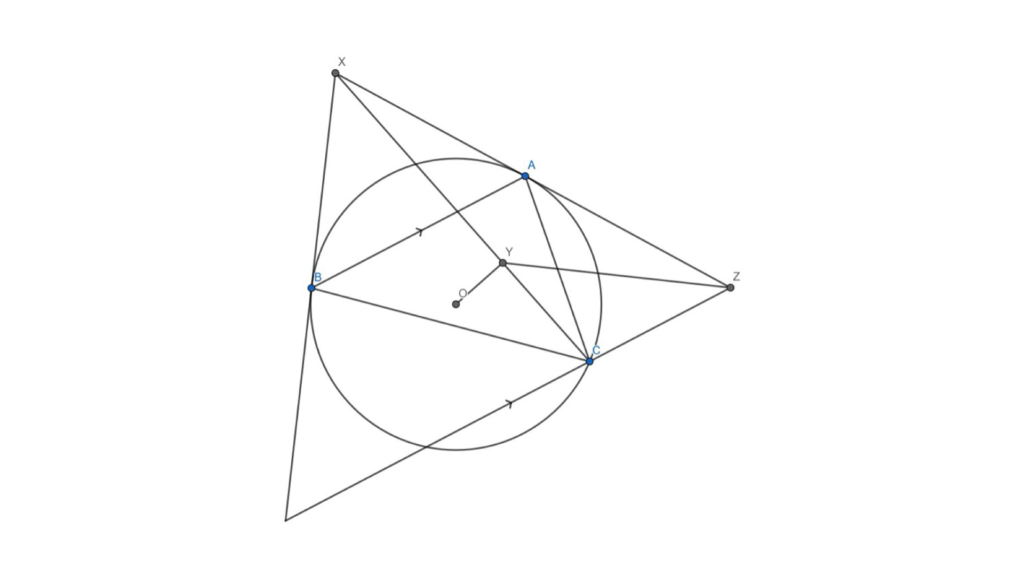
Figure 4: If YZ looks like it goes through the midpoint of AC, then you’ve probably drawn the diagram correctly.
We will begin by showing that triangles ABC and CAZ are similar. We know that ∠BAC = ∠ACZ, since AB is parallel to CZ. Also, ∠ABC = ∠ZAC by the alternate segment theorem. We have two equal angles in these triangles, so they must be similar. Note that this also means that ∠BCA = ∠CZA.
We are required to prove that YZ bisects AC. Our strategy should be first setting M to be the midpoint of AB. We may as well let N be the intersection of YZ and AC. If we can show that the whole configurations AMBC and CNAZ are similar, then this will solve the problem.
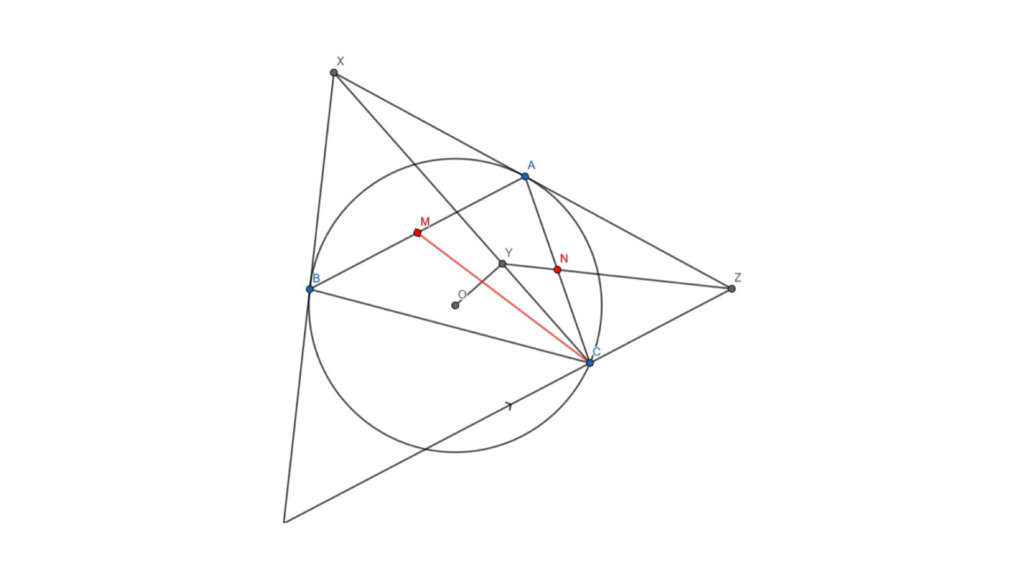
Figure 5: The newly constructed points and lines are in red.
We’ve already shown CAZ is similar to ABC, so it would be sufficient to show that ∠AZY = ∠BCM. This is where isogonal conjugacy comes into play. Notice that CM passes through the centroid of triangle ABC and CX passes through the symmedian point. Recall that the centroid is the isogonal conjugate of the symmedian point, so CX is the reflection of CM over the bisector of ∠ACB. This means that ∠BCM = ∠ACY. We want to prove that ∠AZY = ∠BCM, so it suffices to prove that ∠ACY = ∠AZY. By angles in the same segment, this is true if and only if AYCZ is cyclic.
We will do this by first showing that XBOYA is cyclic. We know that ∠OBX = ∠OAX = 90°, because radii are perpendicular to tangents. This means that ∠OBX + ∠OAX = 180°, so XBOA is cyclic. Also, ∠OYX = 90°, so ∠OBX + ∠OYX = 180°, meaning XBOY is cyclic. This proves XBOYA is cyclic.
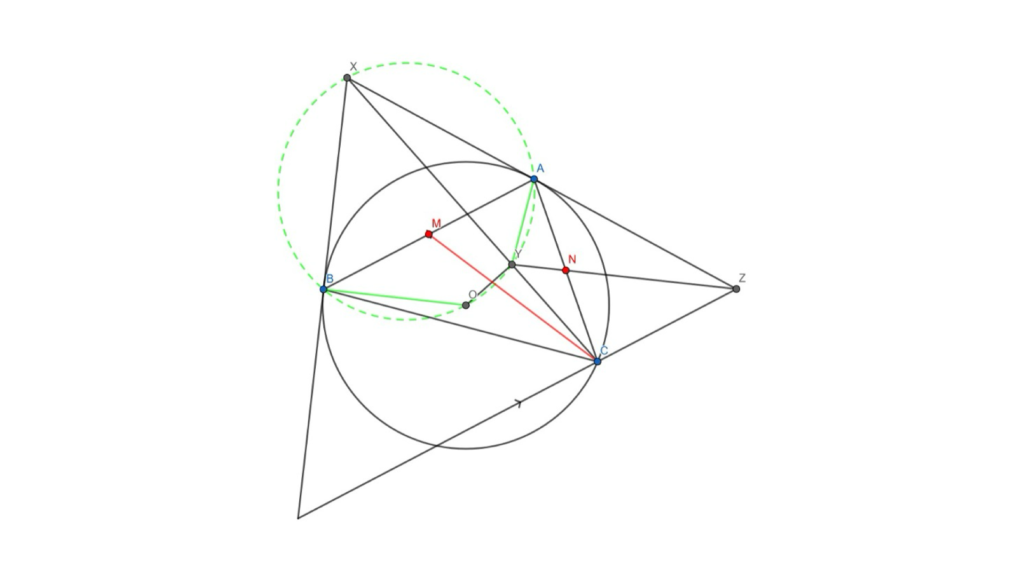
Figure 6: The circle and new lines added are in green.
To finish the problem: ∠CZA = ∠BCA = ∠XBA = ∠XYA = 180° – ∠CYA. The equalities are by the similarity of CAZ and ABC, the alternate segment theorem, angles in the same segment, and angles on a line respectively. This gives ∠CZA + ∠CYA = 180°, which shows that AYCZ is cyclic.
As explained earlier, we can now say that ∠AZY = ∠ACY = ∠BCM, meaning that the configurations AMBC and CNAZ are similar, which shows that N is the midpoint of AC as required.
4 Afterword
It may seem like you would need vast amounts of Olympiad knowledge to solve this problem, but in reality, you don’t need that much. One of the key aspects of olympiad geometry is knowledge of triangle centres. The six main ones are: Incentre, Centroid, Circumcentre, Orthocentre, Nine-point Centre, and Symmedian Point. Learning how these centres are constructed and their key properties, such as which ones are isogonal conjugates of each other, which ones are colinear, and the ratios of distances between them, should be sufficient for many geometry problems. Some problems require no more than GCSE maths to answer, but get their difficulty through the imagination you need to construct certain points which help lead you to a solution.
Furthermore, some of the ideas in this solution may seem unintuitive, and to an extent, like magic. I remember reading a British Maths Olympiad geometry solution, and thinking ”I understand this, but there’s no way I’d ever think of it”. Over the course of this year, I worked my way through the varying diffi- culties of geometry problems, starting with BMO1 problems, then moving onto BMO2 problems, and finally tackling some of the easier ones from international competitions. By regularly chipping away at geometry problems suited to my level, I gradually developed an intuition for the most natural approach to the problem, and start seeing ways I could construct points and lines to assist my solve, picking up required Olympiad knowledge as I did so. As I progressed, I started feeling like I had more control over diagrams, and anything on the page was at my mercy.
If you’re interested in trying out some Olympiad geometry for yourself, or just Olympiad maths in general, then I’d heavily recommend the book A Mathematical Olympiad Primer by Geoff Smith. This is essentially a guide to first round of the British Mathematical Olympiad. The Olympiad’s website also has some fantastic resources. If you start to find yourself obsessed with geometry, then you could get A Mathematical Olympiad Companion, which is similar to the primer, but for second round. Evan Chen’s EGMO book is brilliant for IMO level geometry. Finally, I’d suggest using Geogebra for geometry diagrams, as it’s good to practice doing geometry on paper as well, since this is all you would have in an Olympiad.
