Feature

Building the Towers of Hanoi

/ by Etti B

Etti B

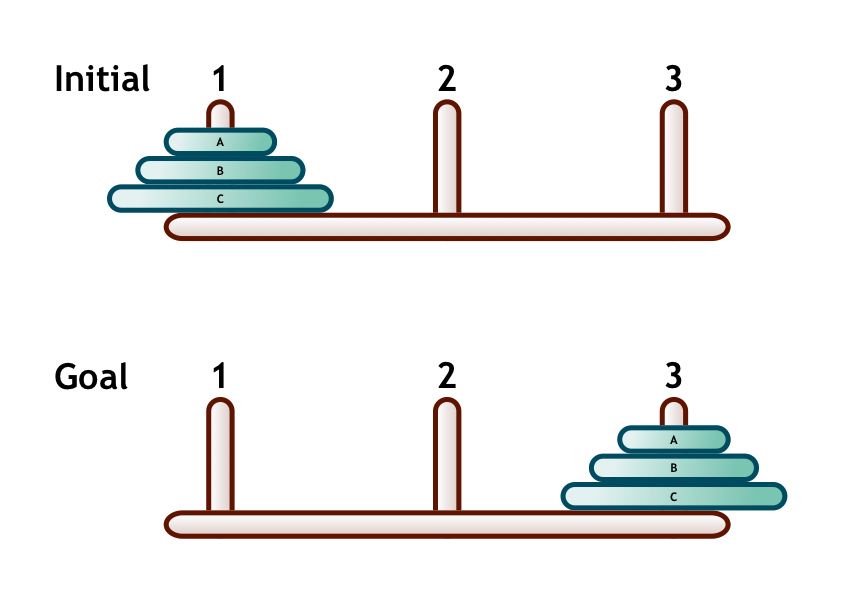
The Towers of Hanoi is a classic puzzle that involves three rods and a number of disks of different sizes. The objective is to move all the disks from the first rod to the third rod, following these simple rules:

  1. Only one disk can be moved at a time.
  2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
  3. No disk may be placed on top of a smaller disk.

The problem was invented by the French mathematician Édouard Lucas in 1883. Lucas created this puzzle as a part of a story about a temple in Hanoi, the capital of Vietnam, where priests were said to be moving 64 golden disks.  According to the legend, once the priests completed their task, the world would end. This dramatic backstory captured people’s imaginations!

The name comes from the story that Lucas created, which features the priests’ moving disks between towers. The “Towers” refer to the three rods, and “Hanoi” connects the puzzle to the temple in Vietnam, making it not just a mathematical challenge, but also a point of cultural interest.

Let’s look at how to solve the Towers of Hanoi puzzle. If you have just one disk, it’s simple — just move it directly from the first rod to the third.

With two disks, you first move the smaller disk to the second rod, then move the larger disk to the third rod, and finally place the smaller disk on top of the larger disk.

So how do you solve it when you have more disks? The solution involves a method called recursion, where you solve smaller instances of the problem. You have to:

  1. Move the top n-1 disks from the first rod to the second rod.
  2. Move the nth (largest) disk to the third rod.
  3. Finally, move the n-1 disks from the second rod to the third rod.

The minimum number of moves required to solve the Towers of Hanoi with n disks is given by the formula 2n – 1. This means for 3 disks, you need 23 – 1 = 7 moves, and for 4 disks, it’s 24 – 1 = 15 moves. This exponential growth shows just how tricky the puzzle can get!

The Towers of Hanoi has connections to computer science, especially in the study of algorithms and recursion. It’s also used in teaching concepts of problem solving and strategic thinking. People have even created giant Towers of Hanoi puzzles as games in parks and playgrounds!

To top