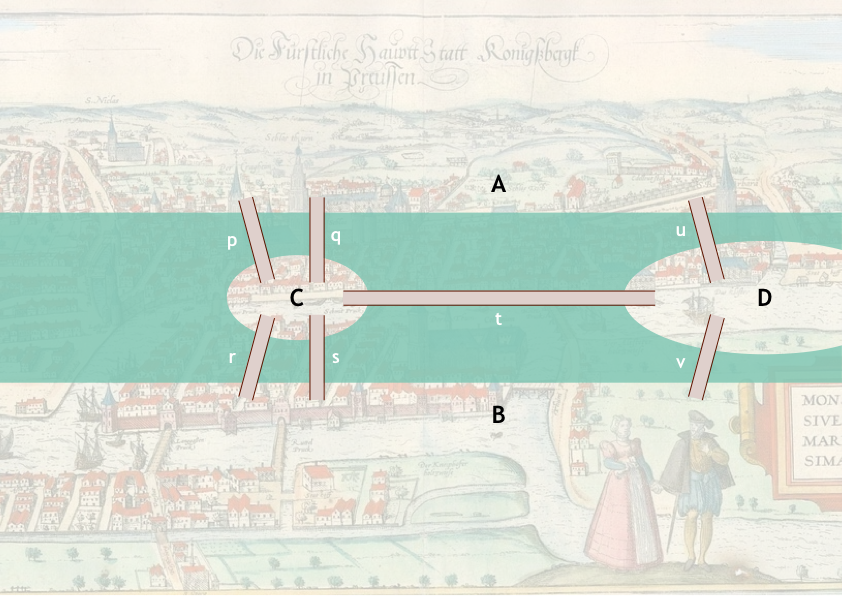
This is the city of Königsberg in the 18th century. The problem was simple: Can you walk through the city and cross each bridge exactly once?
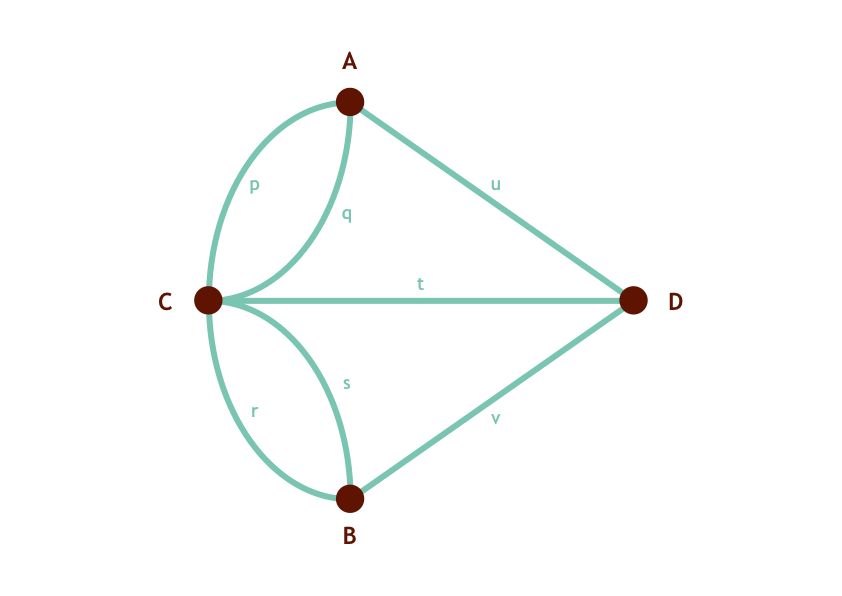
Leonhard Euler realized that the layout of the city wasn’t as important as the connections between landmasses. He converted the problem into a mathematical graph with nodes and edges.
Euler turned the city’s layout into something simpler: a graph. The nodes represent the landmasses, and the edges represent the bridges. This was a major breakthrough for graph theory!
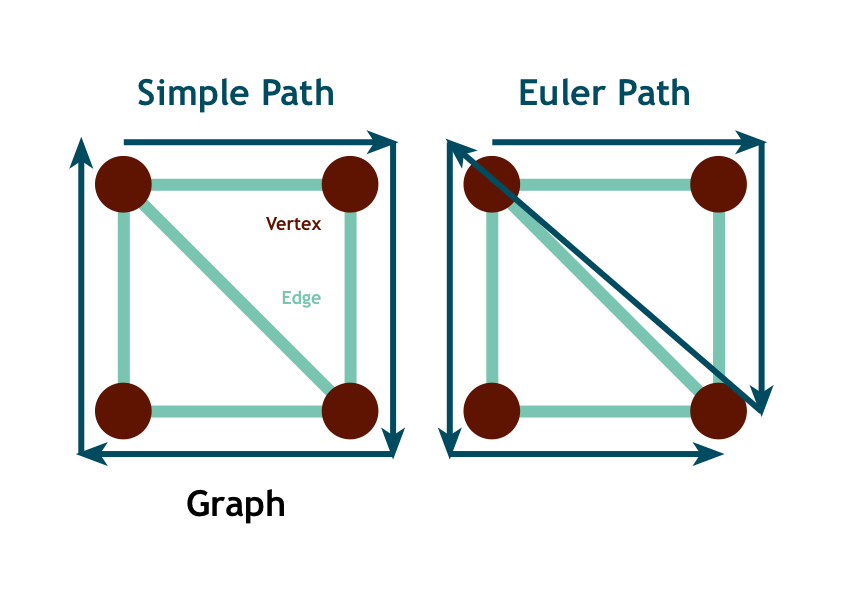
Euler found that for a path to exist where each bridge is crossed exactly once, all the nodes must have an even number of edges, or exactly two nodes can have an odd number.
Euler discovered that the Königsberg problem has no solution because all four nodes have an odd number of edges. Hence, it is impossible to walk through the city crossing each bridge once!