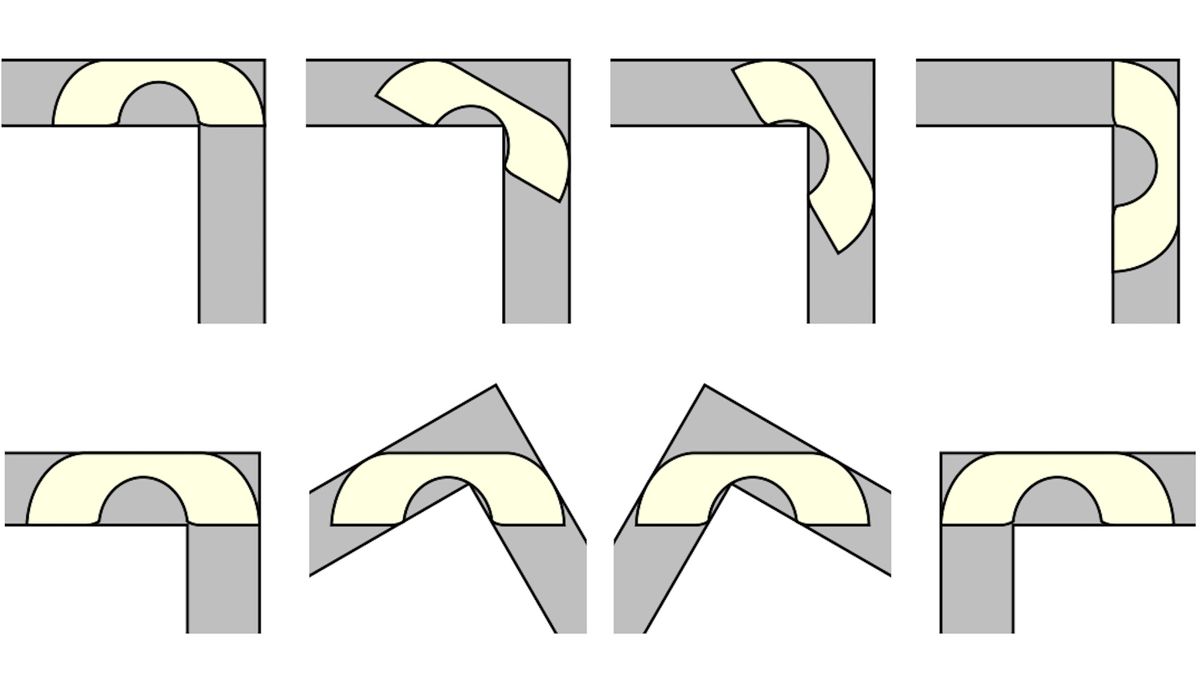
The Moving Sofa Problem is one of the most intriguing and enduring unsolved puzzles in mathematics, sitting at the fascinating intersection of geometry, optimisation, and motion planning. First introduced by Canadian mathematician Leo Moser in 1966, the problem poses a seemingly simple yet surprisingly complex question: What is the largest possible area of a two-dimensional shape that can be manoeuvred around a right-angled corner in a corridor of unit width?
Despite its straightforward statement, this challenge has captivated mathematicians for decades, leading to deep investigations into the nature of shapes, spatial reasoning, and movement.
Understanding the Challenge
To better grasp the Moving Sofa Problem, imagine an L-shaped hallway where both the vertical and horizontal sections are exactly one unit wide. The objective is to determine the shape with the greatest possible area that can navigate the corner without any deformation or lifting. The shape must always remain completely inside the corridor throughout its journey around the corner.
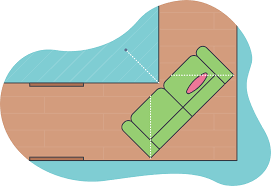
At first glance, it might seem reasonable to assume that simple shapes such as rectangles, circles, or ovals would be optimal candidates. However, researchers quickly realised that irregular, carefully engineered shapes could achieve a larger area while still successfully negotiating the tight turn.
Notable Attempts and Gerver’s Milestone
Over the years, numerous candidate shapes have been suggested and analysed. A significant milestone was reached in 1968 when mathematician Joseph Gerver proposed the shape with the largest known area to date—approximately 2.2195 square units. Gerver’s solution is a remarkably intricate figure composed of 18 separate curve segments, each meticulously calculated to maximise the area while preserving the ability to move through the corner.
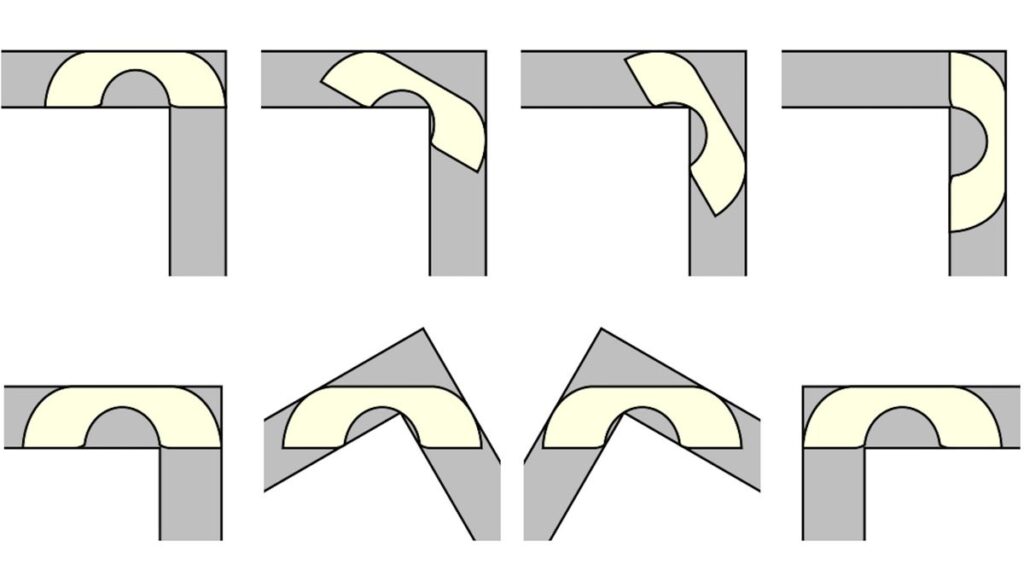
Yet, despite this progress, it remains an open question whether Gerver’s shape represents the absolute optimal solution or if a shape with an even greater area is possible.
Related Problems and Practical Applications
Beyond the core Moving Sofa Problem, related challenges have emerged, enriching the mathematical landscape even further. For instance, the sofa mover’s problem allows the shape to rotate and translate but forbids any deformation, providing a slightly different set of constraints. Meanwhile, the broader piano mover’s problem explores the movement of objects through constrained environments—a field with important practical applications in areas such as robotics, computer graphics, and automated manufacturing.
Understanding the optimal paths and shapes for manoeuvring through tight spaces has direct implications for designing robots and autonomous systems that must navigate complex, confined environments.
A Problem Rooted in Deep Mathematics
Despite its lighthearted name, the Moving Sofa Problem is anchored in deep and sophisticated mathematical principles. It draws upon concepts from calculus, topology, and computational geometry, weaving them into a rich tapestry of geometric optimisation.
The problem highlights the extraordinary difficulty of proving optimality. While it is relatively easy to propose ever-improving shapes, establishing that a particular shape is definitively the best requires ruling out an infinite universe of alternatives.
Ongoing Exploration and Inspiration
Modern mathematicians continue to explore the problem, leveraging advances in computer simulations and algorithmic design to investigate new candidate shapes. The growth in computational power has allowed researchers to model increasingly intricate designs and test them against the corridor’s constraints. Nevertheless, a definitive solution remains elusive.
The Moving Sofa Problem endures as a tantalising challenge, inviting mathematicians, computer scientists, and geometry enthusiasts alike to contribute their insights—perhaps one day unlocking the secret behind this mathematical mystery.
In conclusion, the Moving Sofa Problem stands as a shining example of a deceptively simple yet profoundly difficult question in mathematics. It underscores the beauty, richness, and complexity of geometric reasoning and serves as a testament to the fact that even the most straightforward puzzles can open doors to deep and uncharted mathematical territories.
As long as the problem remains unsolved, it will continue to inspire curiosity, creativity, and rigorous investigation in the quest for mathematical understanding.