Hilbert’s Paradox of the Grand Hotel is a fascinating thought experiment in mathematics, introduced by German mathematician David Hilbert in the early 20th century. It is not a real-life paradox but a clever way to explain the strange and counterintuitive nature of infinity, in particular the kind known as countable infinity. Although it seems simple at first, this idea stretches the limits of how we normally understand numbers, hotels, and logic.
Imagine a hotel with an infinite number of rooms, numbered 1, 2, 3, 4, and so on. Now suppose that every room is already occupied, with one guest per room. In an ordinary hotel, if all the rooms were full, no more guests could be accepted. In Hilbert’s Grand Hotel, however, this is not a problem.

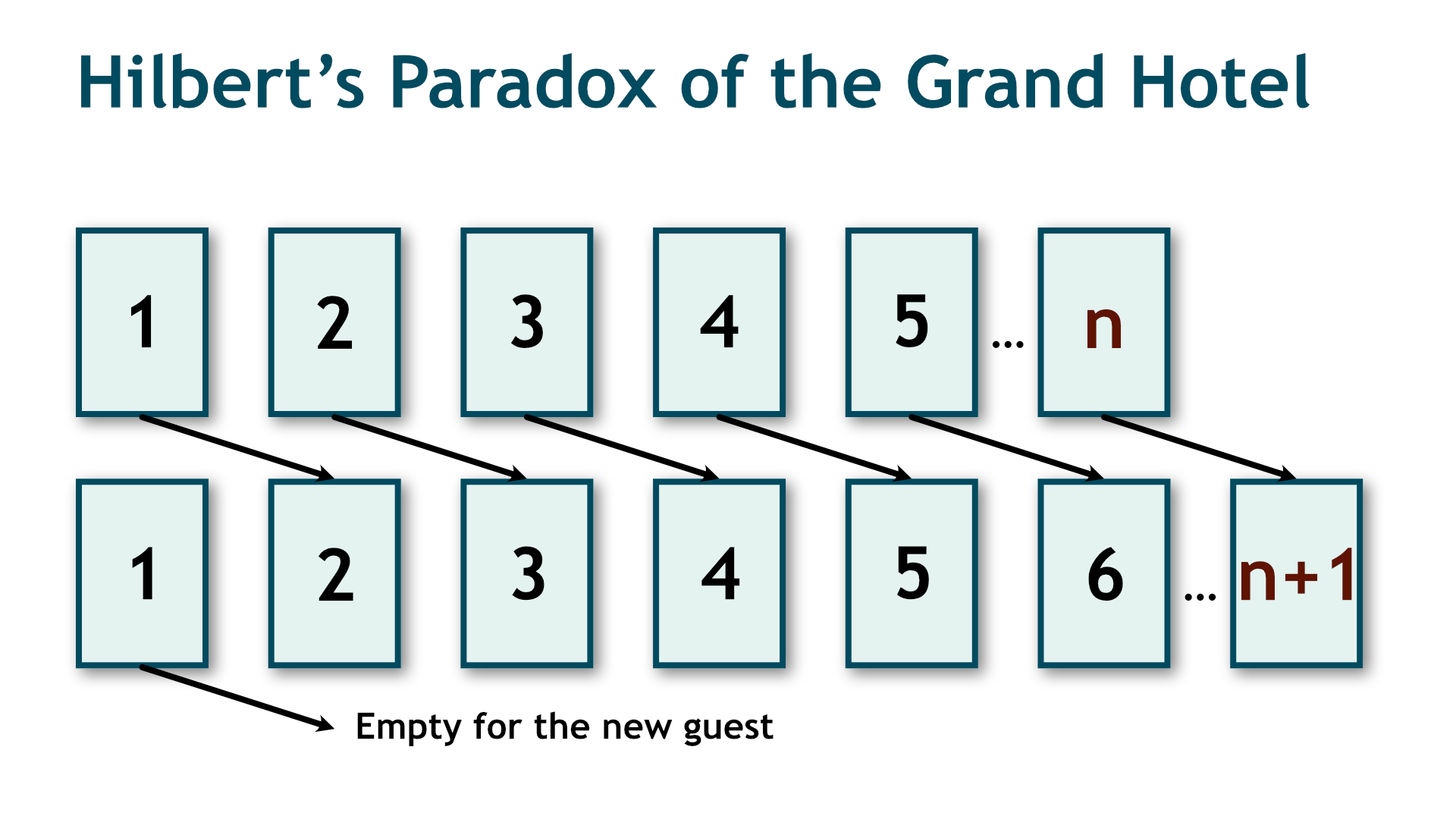
This is where the paradox begins. Suppose a new guest arrives at the reception. It may appear that there is no space, but the manager has a clever plan. They ask the guest in Room 1 to move to Room 2, the guest in Room 2 to move to Room 3, and so on. Each guest moves to the next room. This frees up Room 1, which allows the new guest to check in, even though the hotel was already full.

Now imagine something even more extraordinary: an infinite number of new guests arrive. Once again, there is no issue. The manager instructs each existing guest to move to the room with a number that is double their current one. So, the guest in Room 1 moves to Room 2, the guest in Room 2 to Room 4, the guest in Room 3 to Room 6, and so on. In this way, every even-numbered room becomes occupied, while all the odd-numbered rooms — 1, 3, 5, 7, and so on — are now empty. These are allocated to the newly arrived guests. Even though both groups are infinite, everyone receives a room.
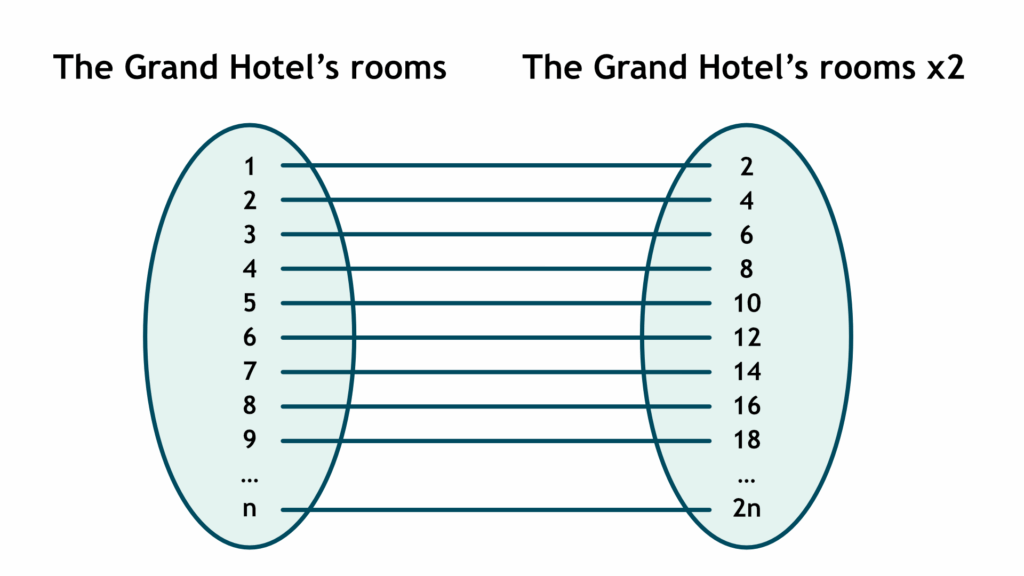
This scenario shows just how strange and unintuitive infinity can be. In everyday life, the word “full” usually means there is no space left. But in the world of infinite numbers, full does not always mean what we expect.
The paradox is used by mathematicians and philosophers to highlight the difference between finite and infinite sets. According to the website Khan Academy, this is an example of a countably infinite set, because you can match every item in the set with a natural number. Britannica explains that Hilbert’s Hotel helps to illustrate some of the concepts behind Georg Cantor’s theory of infinite sets, which revolutionised mathematics in the late 19th century.
Some sources, such as Numberphile on YouTube, even explore how it would be possible to make space for infinitely many infinite buses, each carrying an infinite number of guests. By using patterns and ingenious ways of matching and rearranging numbers, mathematicians show that this, too, can be achieved. This reveals that infinity can come in different “sizes” or levels. One infinity can actually be larger than another — a fact that seems impossible but is entirely valid in mathematics.
Hilbert’s Paradox is more than just a quirky hotel problem. It challenges the way we think about space, numbers, and possibility. It teaches us that mathematics is full of surprises and that, in the strange world of infinity, what appears to be impossible can turn out to make perfect sense.