Ever wondered what a shape with four dimensions would look like? The fourth dimension is an extension of the geometry of space that would give us more ways to move from one place to another. The first dimension would be a line, the only dimension is length. The second dimension would be width, creating a flat plane. When you add depth, you create the third dimension. The fourth dimension is a little bit more complicated.
Is the fourth dimension temporal or spatial?
Einstein believed the fourth dimension was temporal – time. We are always moving forward through time, and it is just as much a dimension as any of the spatial ones, length, width and depth. However, many people now believe that the fourth dimension is spatial.
The spatial fourth dimension
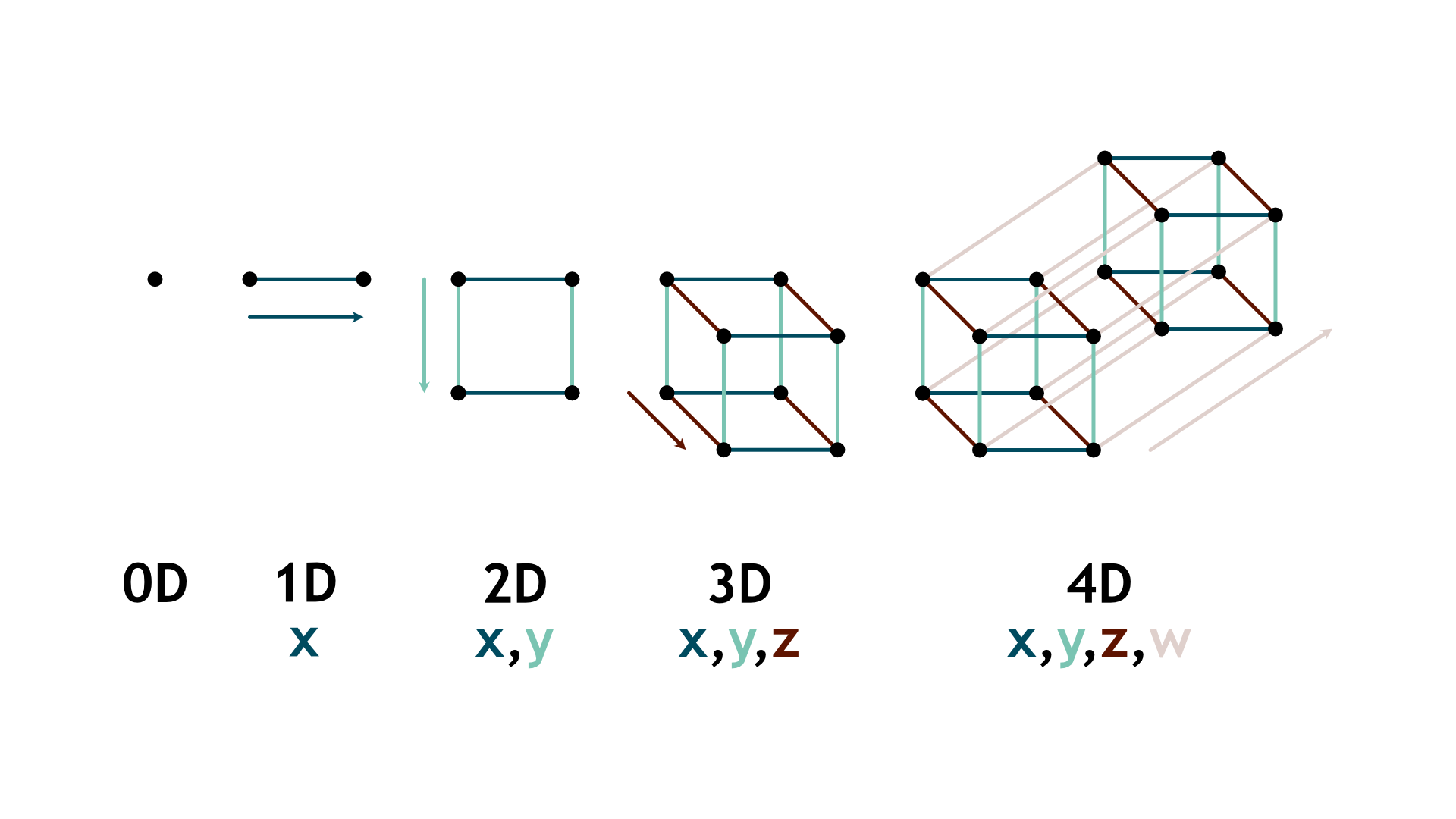
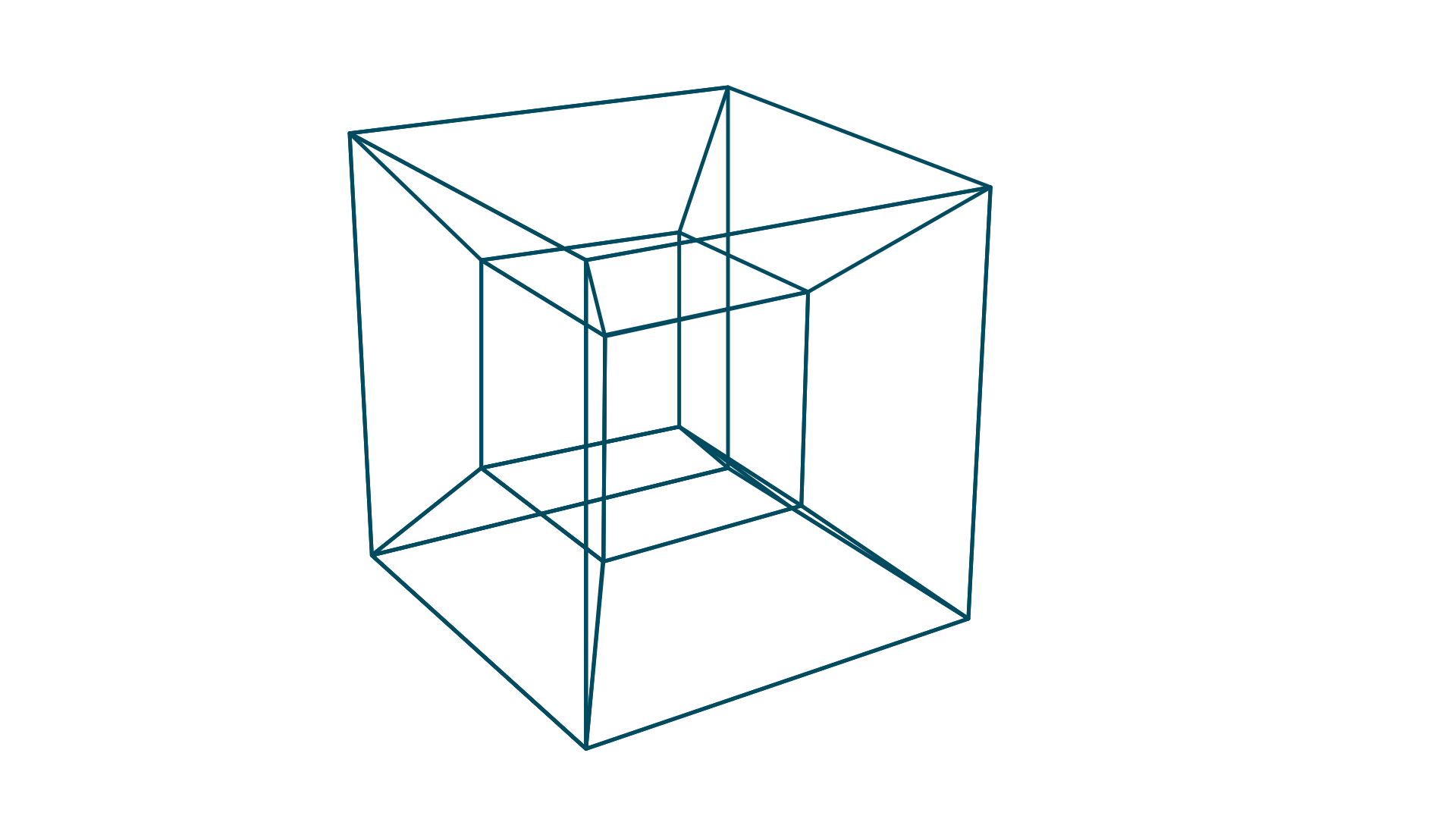
A 1D shape would be a line. The only dimension is width which is shown on the x-axis. To create the second dimension, we would take 2 of these lines (1D shapes) and connect their vertices. This forms a 2-dimensional plane (square) which has width and length. Length is shown on the y-axis. If you now take two squares and connect their vertices together, you will create the third dimension and form a cube (3D shape). A cube has length, width, and depth. Depth is shown on the z-axis. If we follow the same process to create the fourth dimension, we will take two cubes and join their vertices together. This forms a 4D shape called a tesseract.
Every time there is an increase in dimension, there is also an additional direction added. For the first dimension, you have the x-axis, for the second dimension you have the y-axis, and for the third dimension, you have the z-axis. Therefore, for the fourth dimension, you will also need an additional direction, which is perpendicular to every other direction that has been. However, there is not really a line that meets these conditions. This means that for us beings in the three-dimensional world, it is impossible for us to comprehend how a four-dimensional world will look like.
We can understand this better by looking at the two-dimensional analogy. Beings in a two-dimensional world can only see in a straight line (1D). For that reason, if you were to move a 3D object through their eyeline, they would see a weird object that is constantly changing shape. This suggests that theoretically, us 3D beings can only see from a 2D-dimensional perspective, however, we can differentiate between a 3D and 2D object due to the light shone on it. We can use this same theory for 4D beings. In fact, this would mean that a 4D being could see all faces and the inside of a 3D shape at once with their 3D retina. Another pattern with the spatial fourth dimension is that if a cube (3D) is made up of a net of six squares (2D), then a tesseract (4D) is made up of a net of six cubes (3D).
Examples of 4D shapes
Like how the tesseract is a four-dimensional version of a square, a glome is a four-dimensional version of a circle. Another popular example of a 4D shape is the Klein bottle.

In mathematics, the Klein bottle is an example of a non-orientable surface – a one-sided surface which, if travelled upon, could be followed back to the point of origin while flipping the traveller upside down. This is very similar to a Mobius strip, which is also a non-orientable surface. The Klein bottle is constructed from two pieces, one a tube around a figure eight curve and the other a surface of revolution of a piece of that curve, which is created by rotating a curve one full revolution around an axis of rotation.
What is the use of these 4D shapes?
So that is how you create a shape with four dimensions. But why would you? Some theories such as string theory propose our universe has more than three spatial dimensions, that are compactified or hidden from us, and require these additional dimensions to maintain mathematical consistency. We can also use the fourth spatial dimension to solve higher-dimensional problems throughout mathematics, multidimensional scaling in computer science, complex computer networks, game design, protein folding in biomedical research, and navigation in robotics.