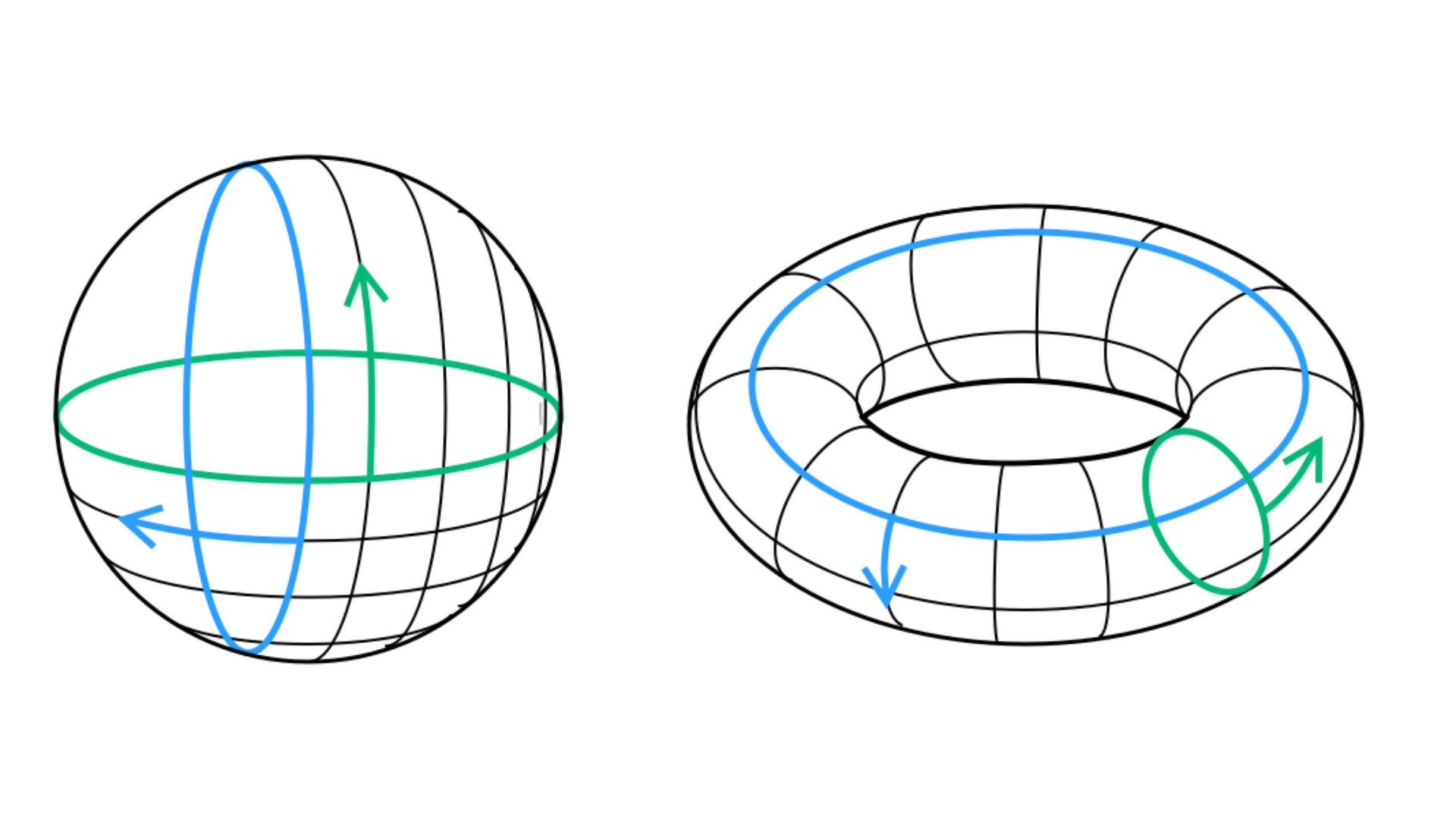
The Poincaré Conjecture, formulated by the great French mathematician Henri Poincaré in 1904, is a central question in topology, the study of shapes that can be stretched or bent without tearing, and the only Millennium Prize problem to have been solved. The core idea is surprisingly simple to state: If a closed, three-dimensional space is simply connected – meaning every loop within it can be shrunk continuously down to a single point – must that space necessarily be equivalent to a 3-sphere.
To understand this, consider the 2D version: a sphere’s surface is the only closed 2D shape where every loop can be shrunk to a point, unlike a donut (torus) where a loop going through the hole can’t be shrunk. Poincaré’s conjecture proposed that this unique property holds true in three dimensions as well. Proving this was one of the greatest mathematical challenges of the 20th century, finally confirmed by Grigori Perelman in the early 2000s using sophisticated new methods.

Mathematical significance and the geometrization breakthrough
The solution to the Poincaré Conjecture is monumental because it wasn’t solved in isolation; Perelman proved the much broader Thurston Geometrization Conjecture.
This larger theorem provides a complete classification system for all 3-dimensional shapes (3-manifolds). It proves that any 3D space can be cut and partitioned into simpler pieces, each of which must have one of eight distinct, uniform geometric structures, like spherical or hyperbolic geometry. The Poincaré Conjecture was simply the specific, crucial case that addressed the properties of the simply connected pieces.
Therefore, the proof didn’t just confirm the uniqueness of the 3-sphere; it provided mathematicians with a foundational “periodic table” for all possible 3D geometries, fundamentally changing how we approach the study of shape. The key technique used, an evolution of Richard Hamilton’s Ricci flow, also introduced powerful new analytical tools to geometry, offering a method to “smooth out” lumpy spaces to reveal their true structures.

Importance in the wider world
While the proof doesn’t directly translate into a consumer product, its impact is profound, particularly for theoretical science and the pursuit of knowledge.
First, in cosmology, the conjecture and the Geometrization Theorem provide the essential mathematical framework for debating and modelling the overall global topology of our own universe. Although the universe’s ultimate shape remains an open question, these theorems define the limited set of geometric possibilities that cosmologists must consider when interpreting astronomical data.
Second, like much of pure mathematics, this breakthrough lays the groundwork for future applied fields. The new analytical techniques developed during the proof could eventually find applications in areas like advanced data science (analysing highly complex, multi-dimensional data sets) or theoretical quantum physics where subtle geometric relationships are crucial.
Ultimately, solving this century-old problem is a magnificent triumph of abstract human reasoning, inspiring new generations and affirming the value of tackling the deepest intellectual mysteries.