Ever tried to make the perfect basketball shot or wondered how satellite dishes are shaped just right? The secret lies in quadratic equations, a powerful tool in algebra that helps us understand how things curve, speed up, slow down, or reach a peak.
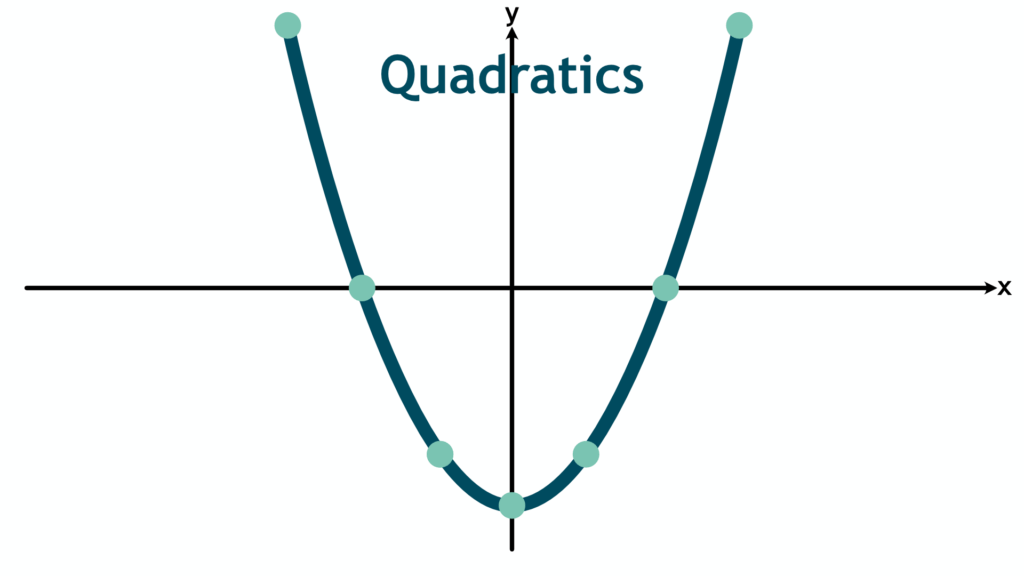
Quadratics are introduced early in secondary school and continue to play an important role in fields like physics, engineering, economics, and computer science. At the core of it all are parabolas, the U-shaped graphs that represent quadratic equations and appear in everything from video games to business models.
The word quadratic comes from the Latin word quadratus, meaning “square”
What is a quadratic?
A quadratic equation is any equation written like this:
ax² + bx + c = 0
Where a, b, and c are constants (and a can’t be zero), and x is the variable. This is called a second-degree polynomial because the highest power of x is 2.
When you graph a quadratic equation, it forms a parabola:
Parabolas are perfectly symmetric, meaning that if you folded the graph in half along its axis of symmetry, both sides would match.
The discriminant, the part under the square root in the quadratic formula, tells you how many real solutions an equation has. If it’s greater than zero, it has two real solutions. If it equals zero, it has one real solution. If it’s less than zero it has no real solutions, but two complex ones.
Solving quadratic equations
To solve a quadratic equation means finding the x-values, called roots or solutions, that make the equation true, that is, the values where the graph crosses the x-axis.
These solutions can represent real-world things, like how long a ball stays in the air, when two vehicles cross paths, or what value a business breaks even at.
Common Methods of Solving Quadratics
- Factoring: Split the equation into two parts that multiply to zero Example: x² + 5x + 6 = 0 becomes (x + 2)(x + 3) = 0 Then solve: x = -2 or x = -3
- Quadratic Formula: A reliable formula that works for every quadratic x = (-b ± square root of (b² – 4ac)) divided by 2a
- Completing the Square: Rearrange the equation into a perfect square Example: x² + 6x + 5 becomes (x + 3)² – 4 = 0
- Graphing: Plot the quadratic on a graph and find the x-values where it touches or crosses the x-axis
Each method shows where the curve hits the horizontal axis – those points often tell us when something starts, stops, or reaches a goal. Understanding the shape of the curve helps you figure out key moments in whatever situation you’re analysing.
Key features of a parabola

- Vertex: The highest or lowest point (depending on the direction of the curve)
- Axis of Symmetry: The vertical line that cuts the parabola in half, Formula: x = -b divided by 2a
- Roots or Solutions: The points where the curve crosses the x-axis (y = 0)
- Y-Intercept: Where the parabola crosses the y-axis (when x = 0); this is equal to c
The vertex is often key in real life, it might tell you the maximum height of a rocket, the minimum cost of a product, or the best angle to launch something at.
Why quadratics matter
Quadratics aren’t just for maths exams, they’re all around us. In physics, they model falling objects, projectiles, or acceleration. Engineering uses them to design bridges, parabolic mirrors, or reflector dishes. In business and economics, quadratics are used to find the most profitable points or the lowest costs. Quadratics are used in computer graphics for smooth animation, curved motion, and collision detection. They are also used in video games to simulate jumps, gravity, and arcs.
From engineering challenges to everyday problems, quadratics help us make predictions, optimise designs, and understand the world in motion. Whether you’re solving equations for homework or designing the next game physics engine, understanding how parabolas work is both practical and exciting.