Trigonometry
Have you ever wondered how your phone calculates your exact location? Or how architects ensure that bridges don’t collapse? These aren’t just cool feats of engineering – they’re powered by trigonometry, the branch of mathematics that studies the relationships between angles and lengths in triangles.
The origins of trigonometry stretch back thousands of years. Ancient Egyptians and Babylonians used basic trig ideas to measure land and track celestial objects. The Greeks, especially Hipparchus and Ptolemy, developed early trigonometric tables. Later, scholars in the Islamic Golden Age formalized sine, cosine, and tangent functions. Today, trigonometry underpins technologies in GPS, medical imaging, game development, and even astrophysics.
Aryabhata, an Indian mathematician from the 5th century, used sine tables centuries before they appeared in Europe.
The basics: from triangles to circles
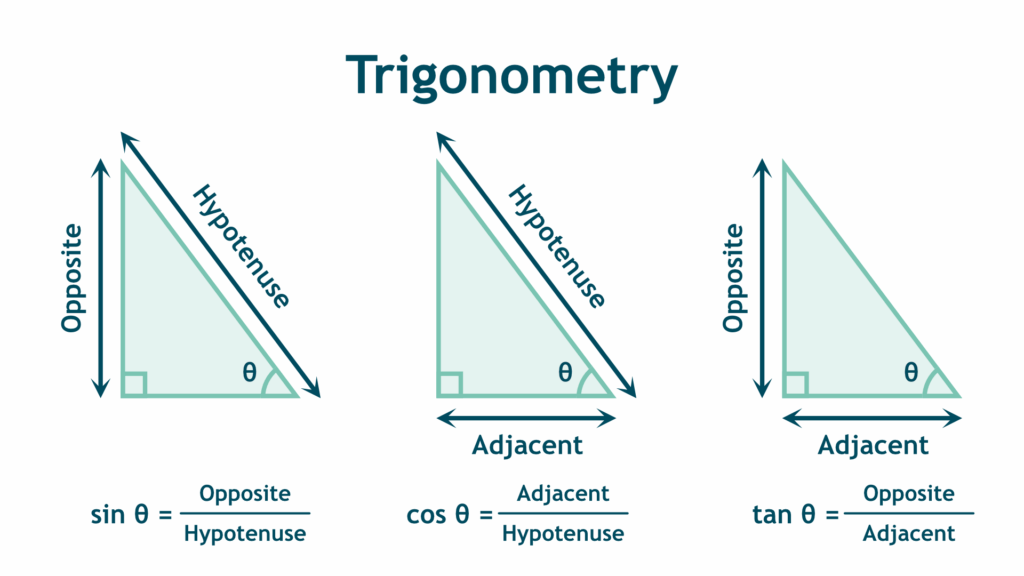
At its core, trigonometry is about right-angled triangles, those with a 90° angle. It provides tools for finding unknown sides or angles using three primary functions:
- Sine (sin θ) = Opposite / Hypotenuse
- Cosine (cos θ) = Adjacent / Hypotenuse
- Tangent (tan θ) = Opposite / Adjacent
The word ‘sine’ comes from a Sanskrit word jya, which was mistranslated through Arabic and Latin.
You might remember this with the mnemonic SOHCAHTOA. For example, if a ladder leans against a wall, trig can help calculate how far up the wall it reaches or how far its base is from the wall.
But trig doesn’t stop at right triangles. It extends to non-right triangles using:
- The Sine Rule: a / sin(A) = b / sin(B) = c / sin(C)
- The Cosine Rule: c² = a² + b² − 2ab * cos(C)
These rules are vital for solving for angles and sides of triangles when you don’t have a right angle.
Core concepts
The unit circle
- The x-coordinate of a point on the circle is cos θ
- The y-coordinate is sin θ
This approach helps explain how trig functions behave with angles greater than 90°, including negative angles and those beyond 360°.
Trigonometric Graphs
The graphs of sine, cosine, and tangent show how these functions vary:
- Sine and cosine wave smoothly between -1 and 1.
- Tangent increases sharply and has vertical asymptotes where it’s undefined.
Understanding these graphs helps with modeling periodic behavior, like sound waves or day-night cycles.
Key Identities and Equations
Some identities you’ll encounter include:
- sin²(θ) + cos²(θ) = 1
- tan(θ) = sin(θ) / cos(θ)
- Angle addition formulas, like: sin(θ + φ) = sin(θ) * cos(φ) + cos(θ) * sin(φ)
These identities are essential for solving complex problems and proving relationships between expressions.
Patterns, proofs, and deeper ideas
Trigonometry reveals elegant mathematical structures. For example, the identity: sin(θ + φ) = sin(θ) * cos(φ) + cos(θ) * sin(φ) is the equation of a unit circle—connecting geometry and algebra.
Addition formulas, like: cos(θ + φ) = cos(θ) * cos(φ) − sin(θ) * sin(φ) allow us to evaluate trig functions for combined angles, crucial in physics and signal analysis.
There’s also Euler’s Formula: e^(iθ) = cos(θ) + i * sin(θ). This stunning identity ties together exponential functions, imaginary numbers, and trigonometry. It’s considered one of the most beautiful equations in mathematics.
Real-World Applications of Trigonometry
Trig has applications far beyond the classroom:
- Engineering: Structural analysis, bridge design, and flight control systems
- Physics: Modeling wave motion, oscillations, and light behavior
- Computer Graphics: 3D rendering, lighting, and animation
- Medicine: CT scans, ultrasound imaging, and heart rate monitoring
- Navigation: GPS technology, radar systems, and astronomy
Even music and electronics use trig to analyse signals and compress data.
Trigonometric functions power Fourier analysis, used in everything from JPEG image compression to audio engineering.
The power of trigonometry
Trigonometry starts with triangles but scales up to circles, waves, and even imaginary numbers. It’s a bridge between geometry, algebra, and real-world problem-solving. Whether you’re studying motion, modeling sound, or building the next big tech innovation, trig gives you the mathematical tools to explore and understand the world more deeply.