The Fibonacci Sequence
Mathematics is filled with fascinating patterns, from the famous Fibonacci sequence and the golden ratio to regular arithmetic sequences. These mathematical structures often appear in places that seem entirely random, revealing an underlying order in the world around us.
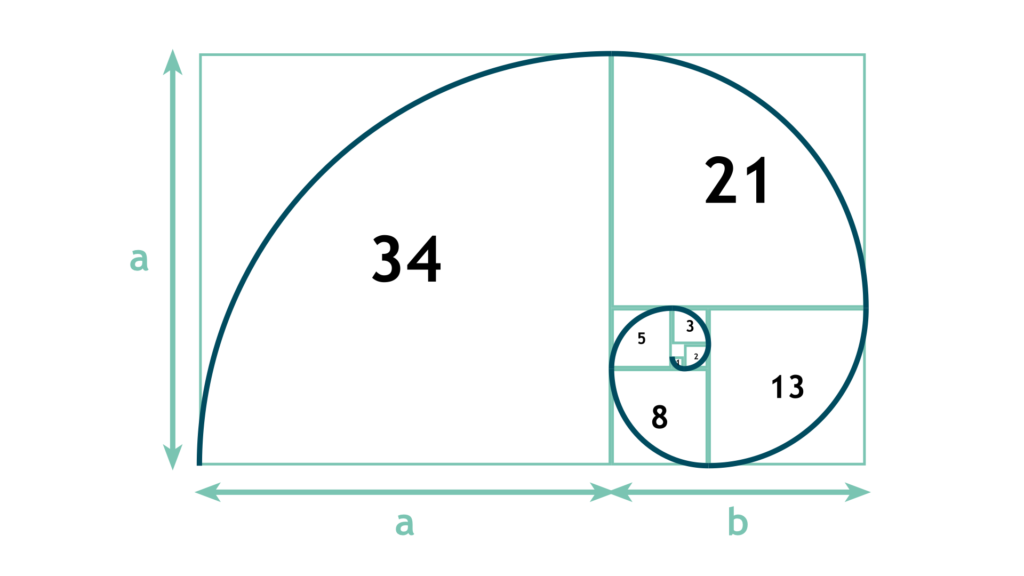
The Fibonacci Sequence is a simple yet profound numerical pattern in which each term is the sum of the two preceding numbers. It is one of the most renowned mathematical sequences globally:
1, 1, 2, 3, 5, 8, 13, 21, 34…
From its origins in ancient Indian mathematics to its introduction to Western mathematics by Leonardo Fibonacci, this sequence has shaped modern mathematical thought.
There is a scientific journal dedicated to Fibonacci numbers, first published in 1963 by the American Fibonacci Association, called Fibonacci Quarterly.
The Golden Ratio
The golden ratio, often represented by the Greek letter phi (ϕ), is a mathematical constant approximately equal to 1.618. It describes a proportion in which two numbers, a and b, relate such that the ratio of a to b is the same as the ratio of a+b to a.
Throughout history, this ratio has been known by various names, including the divine proportion and the golden cut.
The Golden Spiral: Where Fibonacci Meets the Golden Ratio
The golden spiral is a logarithmic spiral whose growth factor is equal to the golden ratio. With every quarter turn, the spiral expands by a factor of ϕ.
Interestingly, the Fibonacci sequence is closely linked to the golden ratio. If you take a term in the Fibonacci sequence and divide it by the previous term, the result approaches the golden ratio as the sequence progresses.

The Fibonacci spiral, formed by constructing squares with side lengths corresponding to Fibonacci numbers, serves as a close approximation of the golden spiral. This connection highlights the deep mathematical relationship between these two patterns.
Pascal’s Triangle
Pascal’s triangle is a triangular array of numbers named after the 17th century French mathematician Blaise Pascal. However, its fundamental principles were studied long before his time.
Each number in the triangle is the sum of the two numbers directly above it. This simple structure holds many mathematical properties and applications, including its role in binomial expansion.
Surprisingly, the Fibonacci sequence is also hidden within Pascal’s triangle. If the triangle is arranged as a right-angled structure and the sums of diagonals are taken, the Fibonacci sequence emerges.

The Fibonacci sequence is hidden within Pascal’s triangle. When arranged as a right-angled triangle, the sums of diagonals form Fibonacci numbers.
Mathematical Patterns in Nature
Over thousands of years, nature has evolved to optimise key factors, often following mathematical sequences.
The Fibonacci sequence appears in the arrangement of leaves, flowers, and seeds in plants, helping them maximise space and sunlight exposure. It was originally discovered as a model for rabbit reproduction and has since been observed in various animal breeding patterns.

The golden ratio is evident in nautilus and mollusc shells, which follow logarithmic spirals approximating ϕ. It also appears in human anatomy, where proportions such as the ratio between the hand and forearm tend to follow the golden ratio.

Celebrated annually on 23 November, Fibonacci Day honours the Fibonacci sequence. Written in the MM/DD format, the date appears as 11/23, matching the first four Fibonacci numbers.
The Relevance of Mathematical Patterns
Beyond nature, these core mathematical patterns play a crucial role in various disciplines, helping us understand the world more deeply.
In art and architecture, the golden ratio is used to create aesthetically pleasing designs and proportions, influencing room and window dimensions.
In computer science, the Fibonacci sequence is often the first recursive function that new programmers write, due to its self-referential nature.
The more we explore, the more these mathematical patterns reveal themselves in unexpected places.
