You might just think of prime numbers as those few, weird irregular numbers only divisible by themselves and 1. But this very property makes them the basis of our entire number system, and there are plenty of mysterious and wonderful properties of these prime numbers and the patterns they create to explore.
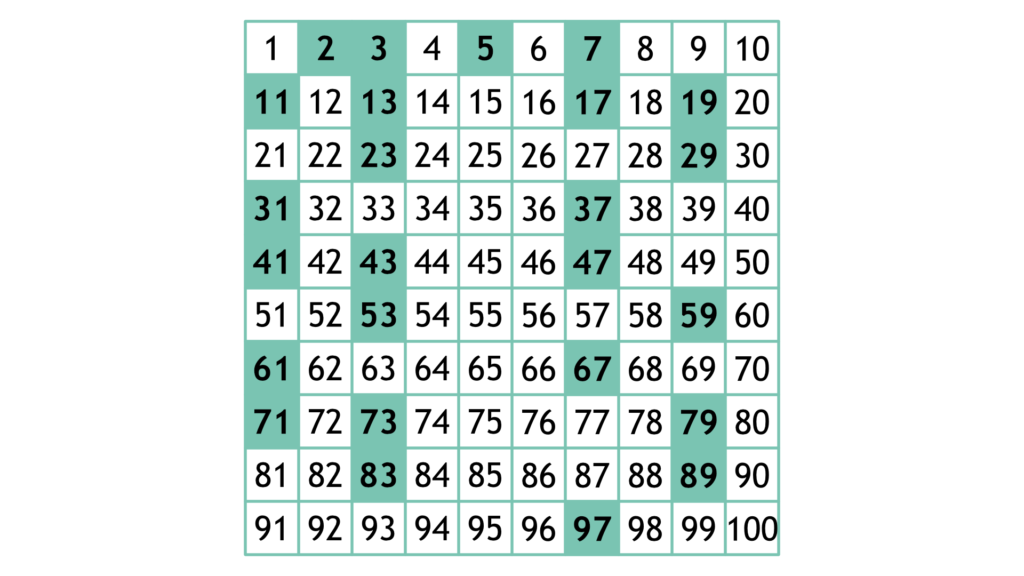
So first of all, what are prime numbers? They are natural numbers that only have two positive divisors, numbers they can divide cleanly by. They are commonly defined as only being divisible by themselves and 1, however 1 is and yet is not considered a prime number. The first few prime numbers are 2, 3, 5, 7, 11, 13, 17 and 19. Each prime is unique in that it cannot be made by multiplying two smaller natural numbers.
Many famous mathematical problems and theorems, not least The Riemann Hypothesis (and its $1 million reward for a proof) and Goldbach’s Conjecture, even the Fundamental Theorem of Arithmetic, revolve around prime numbers. The latter states that every integer greater than 1 can be uniquely factored into a product of prime numbers. Primes are also crucial for modern encryption methods.
However, perhaps the patterns the distribution of primes creates is even more fascinating.
Prime Spirals
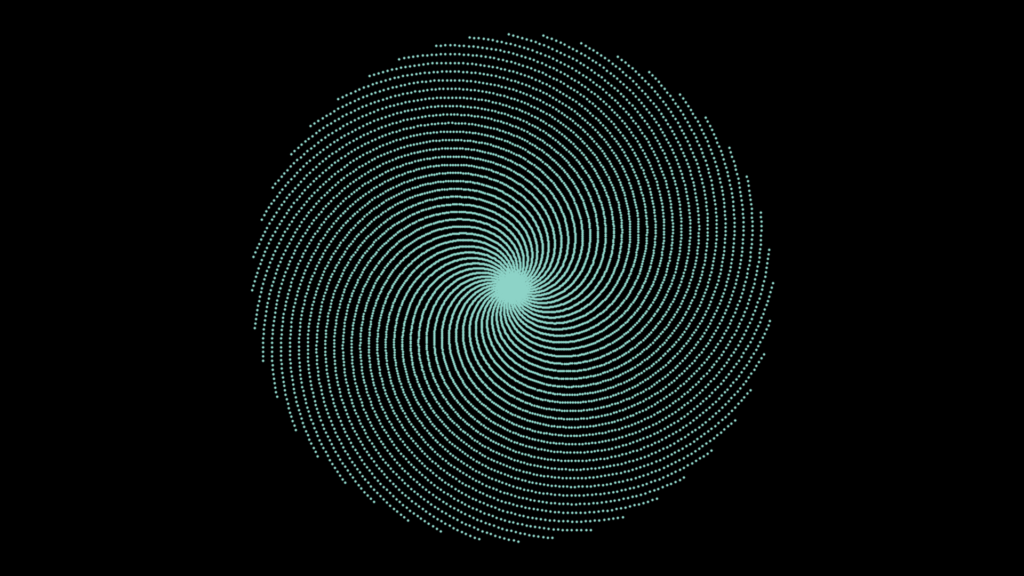
Although primes are famous for their chaotic nature, it’s actually possible to find patterns within the distribution of primes. There are many examples of ‘prime spirals’, that plot prime numbers on graphs to create a fascinating array of points that appear almost magically aligned.
An example is the Ullam Spiral, where a square lattice is used to mark all the integers in a spiral arrangement, and all of the prime numbers are separated and plotted on a graph, to look like shown. There have been many examples of computers plotting hundreds of thousands of primes on the Ullam Spiral, and determining any links within its patterns, of which many have been found, like how lines in the pattern corresponds to 4n2 + bn + c.
There are also variations of these spirals, like a Sack Spiral, which is plotted on an Archimedean spiral, named after mathematician Archimedies, using Polar Coordinates, that creates a different circular series of patterns, and even triangular forms of the spiral, which highlight the reason mathematicians are still dazzled by primes to this day.
Did you know that one of the first mathematical algorithms ever created was used to find prime numbers up to a limit? In the 3rd Century BCE, an ancient greek mathematician named Erathosthenes determined how to search for prime numbers in a data set through a “sieve”, which is now named after him. In this method, every number from 2 to the limit of the range is written down. You will then remove the multiples of the first number: 4, 6, 8, 10, and so on. This will then be repeated on the next unmarked number, like 3. When you have reached the end of the numbers in the category, you have successfully found all the prime numbers in the range using an algorithmic approach.
Fermat Primes
Fermat primes are an incredible, rare, special category of prime that was originally studied by Pierre de Fermat, best known for his Last Theorem. Fermat Primes are positive prime numbers where Fn = 2(2^n) + 1, where n ≥ 0. Not many of these exist, with only 5 being mathematically known, these being 3, 5, 17, 257, and 65537, with more not yet mathematically confirmed.
These numbers may seem arbitrary and just appear to be a cool mathematical fact, but it turns our these actually have mathematical uses. Although not present in nature like the golden ratio, or Fibonacci sequence, it turns out that they actually have a large impact on cryptography and digital signal processing. This allows our modern online world to run smoothly, and exemplifies the wonders of primes.
This article is still being developed and may be updated or expanded in the future.