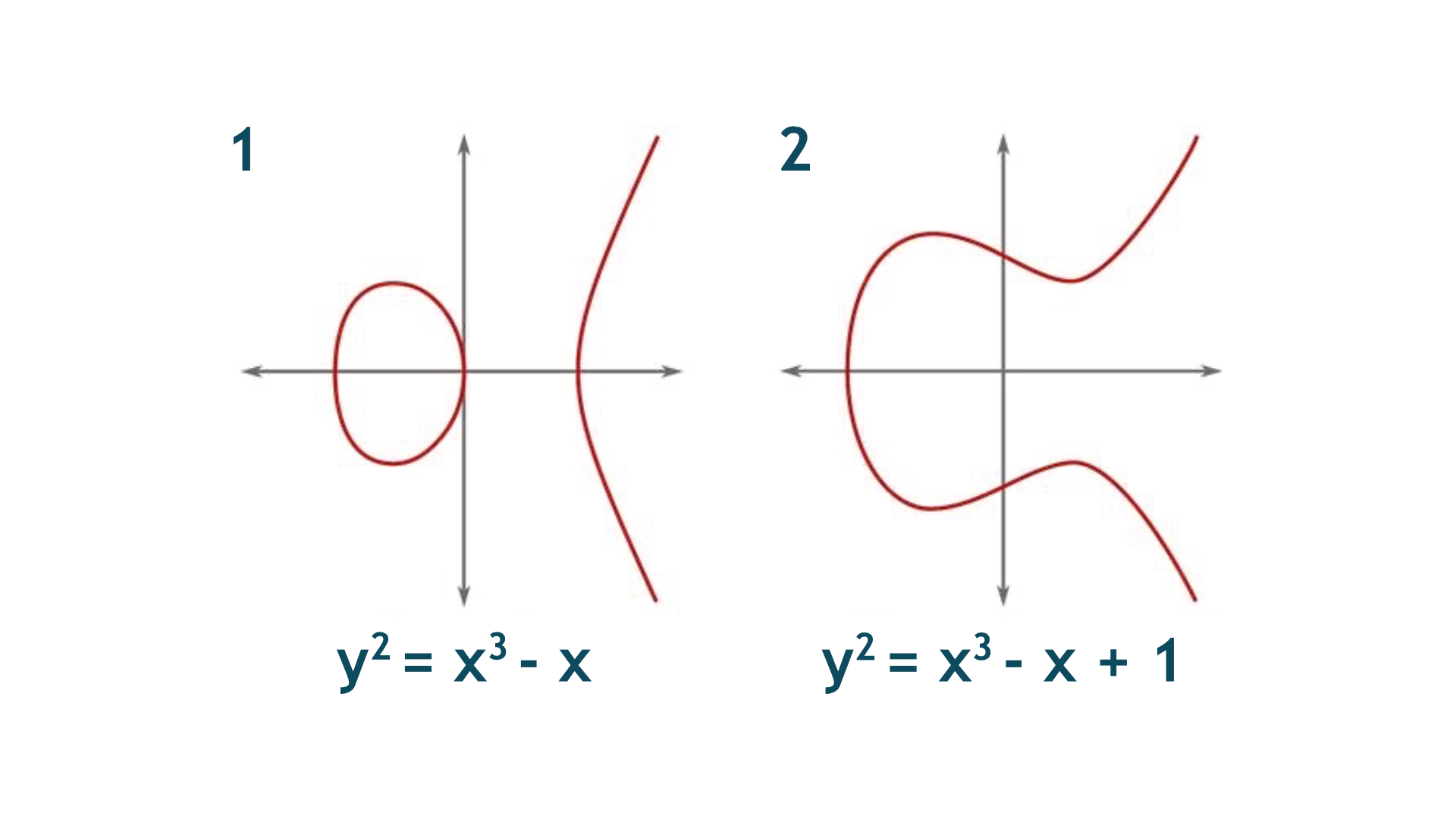Sitting at the heart of the Clay Mathematics Institute’s seven Millennium Prize Problems, each carrying a bounty of $1 million, is the Birch and Swinnerton-Dyer (BSD) Conjecture, a riddle that proposes a stunning connection between two seemingly unrelated universes of mathematics – algebraic geometry and complex analysis.
The problem centres on elliptic curves which are defined by relatively simple equations like y2 = x3 + ax + b, appearing visually as smooth, looping lines on a graph. While these curves look innocuous, they harbour a deep secret regarding rational points, solutions where both x and y are simple fractions or integers.
For thousands of years, mathematicians have struggled to determine if a specific curve has a finite number of these rational solutions or an infinite set generated by a few starting points. In the 1960s, mathematicians Bryan Birch and Peter Swinnerton-Dyer used early computers to test thousands of these curves and discovered a mysterious pattern – the number of rational solutions seemed to be perfectly dictated by the behaviour of a completely different mathematical object called the L-function (a complex function like the Riemann Zeta function).
The conjecture posits that if the value of a curve’s L-function vanishes (equals zero) at a specific point (s=1), then the curve possesses an infinite number of rational solutions. Furthermore, the ‘order’ of that zero tells us exactly how many independent families of solutions exist. This is not just abstract theory – it underpins the logic of Elliptic Curve Cryptography (ECC), the modern security standard that protects everything from your credit card transactions to WhatsApp messages.
By proving the BSD Conjecture, we wouldn’t just be earning a million dollars. We would be confirming the power of the mathematical bridge that secures our digital reality, proving that the abstract world of complex functions dictates the concrete ‘hard’ algebra of number theory.