Pi: The most important constant?
Kai G and Charlton C
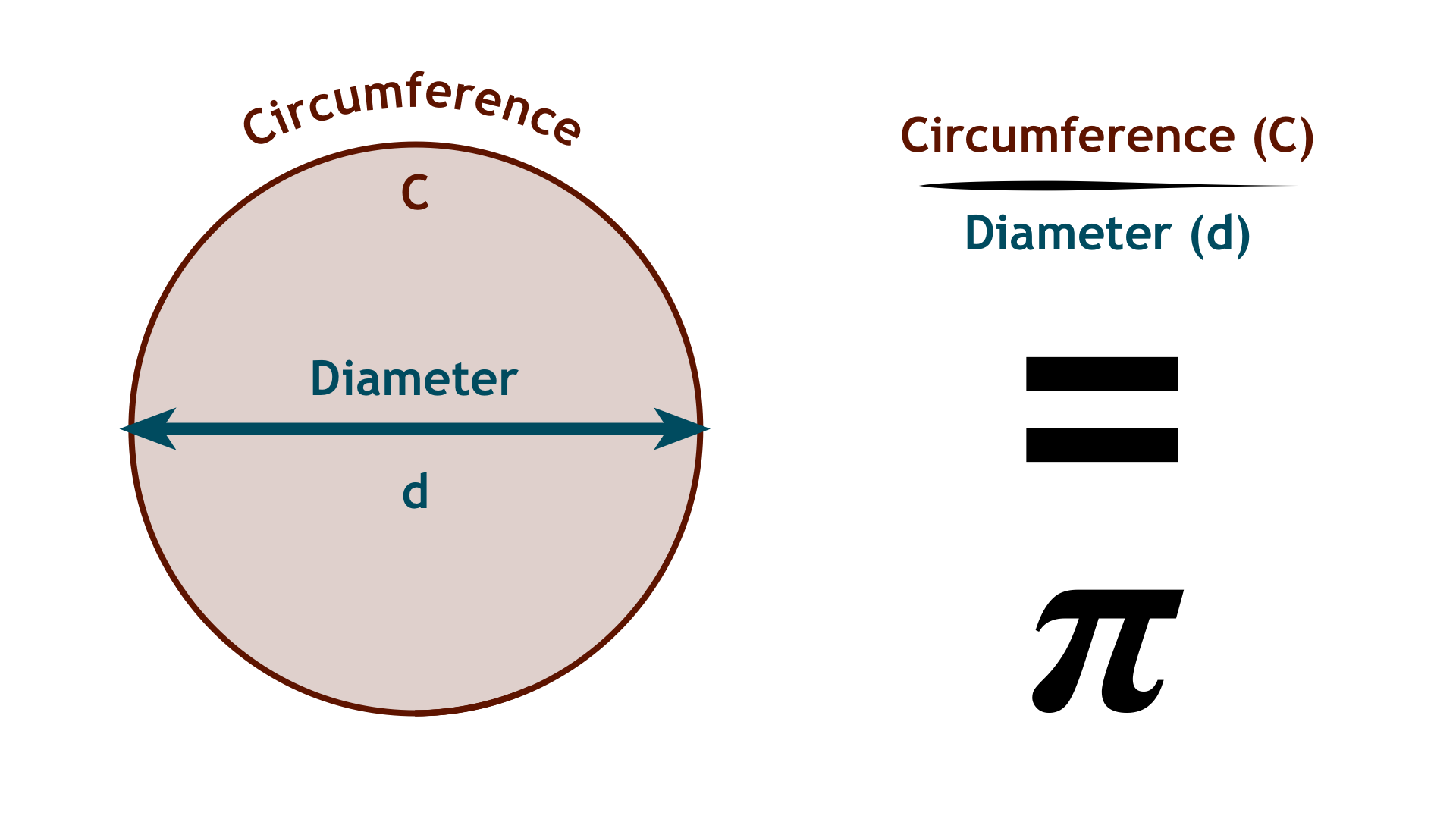
You’ve probably come across Pi in the context of circles. A circle is a shape consisting of all the points in a plane that are at a given distance, the radius, from the given point, the centre. The diameter is twice the radius, defined as a line segment between two endpoints that lie on the circle passing through the centre. The distance around the circle is its circumference.
Pi can be defined as the ratio between the circumference and diameter of a circle, which is always the same. Pi is defined by an infinite decimal expansion, meaning that it has an infinite number of digits, and cannot be expressed exactly as a ratio. This makes it an irrational number, a fact first discovered by Johann Heinrich Lambert in 1761. This means we can only approximate it, which is why in equations it is represented by the symbol π. Pi is also transcendental, meaning that Pi is not the root of any algebraic equation with rational coefficients. It even has its own holiday!
Why Pi? The letter π is the first letter in the Greek word for “periphery”, the “periphery” of a circle being the precursor to the “perimeter” of a circle, which today we call a circle’s circumference. Welsh mathematician William Jones chose the Greek letter as the constant’s symbol in 1706, but it was mostly popularised by the great Leonhard Euler, who adopted it in 1737.
Pi is an ancient mathematical curiosity
The constant has, of course, not always been called Pi. People have known about, and been intrigued by Pi for a long time. Almost 4,000 years. The ancient Babylonians calculated the area of a circle by multiplying the square of its radius by three. One of their tablets from around 1900–1680 BCE indicates they approximated Pi to 25/8, a value of 3.125. The famous Egyptian Rhind Papyrus, from around 1650 BCE shows the Egyptians could calculate the area of a circle by a formula that gave the approximate value for Pi as 3.16045, which is even closer to the real value.
Pi is actually a part of Egyptian mythology. People in Egypt believed that the pyramids of Giza were built on the principles of pi. The vertical height of the pyramids have the same relationship with the perimeter of their base as the relationship between a circle’s radius and its circumference. The pyramids are phenomenal structures and are one of the seven wonders of the world.
Archimedes of Syracuse, in Sicily, who lived from 287 to 212 BCE, used the Pythagorean Theorem and regular polygons to approximate the shape of a circle. He recognised that he had not found the exact value but showed it to be within 3 1/7 and 3 10/71. In the fifth century, brilliant Chinese mathematician and astronomer Zu Chongzi estimated the value of Pi to be 355/113. That is a number that starts 3.141592… which is correct to six decimal places. To be this accurate, he must have started with a regular polygon with 24 thousand 576 sides and performed calculations with hundreds of square roots to 9 decimal places. In the early twentieth century, the Indian mathematician Srinivasa Ramanujan established several formulae for calculating Pi. His approach forms the basis of some of the fastest algorithms used to calculate Pi. The first term of the series gives a value that is correct to six decimal places. The first two terms give a value correct to 14 decimal places.
The calculation of Pi is a stress test for a computer. It works just like a digital cardiogram since it indicates the level of activity within the computer’s processor.
Computers revolutionised the accuracy with which we could predict Pi. In 1948, Ferguson and Wrench achieved a result correct to 808 places. In December 2002, 10 mathematicians led by Professor Yasumada Kanada took more than a hundred hours of computer time to calculate the value of Pi correctly to an incredible 1.24 trillion digits.
3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679
Pi to 100 digits
Why is Pi useful?
Pi allows you to find the circumference or area of circle using 2πr and πr2 respectively. This is crucial for basic construction and calculation. Pi is also used to calculate the surface areas and volumes of cylinders, cones and spheres.
| Formula | |
|---|---|
| Area of a Circle | A = πr2 |
| Circumference of a Circle | C = 2πr |
| Volume of a Cylinder | V = πr2h |
| Surface Area of a Cylinder | A = 2πr2+2πrh |
| Volume of a Cone | V = πr2h/3 |
| Surface Area of a Cone | A = πr(r+√(h2+r2)) |
| Volume of a Sphere | V = 4πr3/3 |
| Surface Area of a Sphere | A = 4πr2 |
h = height
You can find out more in our Shapes and Solids notebook guide.
The constant Pi helps us understand our universe with greater clarity. The definition of Pi inspired a new unit of measurement for angles, called radians. 360 degrees is equal 2π radians. A radian is defined as the angle at the centre of a circle for an arc that is the length of the radius. This is useful for navigation, triangulating locations and working out precise distances. Pi is also used in calculus to calculate integrals and derivatives.
It is claimed that Pi even describes the bendiness of rivers. You can measure how “bendy” a river is by measuring its total length and dividing by straight route from its source to mouth, this measure is called “sinuosity”. So a totally straight river would have a sinuosity of 1, while very bendy rivers can have very high sinuosity, with no limit to how high it can go. Yet, it is claimed the average sinuosity of rivers around the world is Pi. This is an incredible fact, and if true means that rivers are typically a little over three times longer than the direct route from source to mouth. Of course some rivers are straighter, and some rivers are longer, but the average sinuosity is around 3.14.
So, it is a good bet you have encountered Pi very often in your life — even if you don’t realise it!
Is Pi actually wrong?
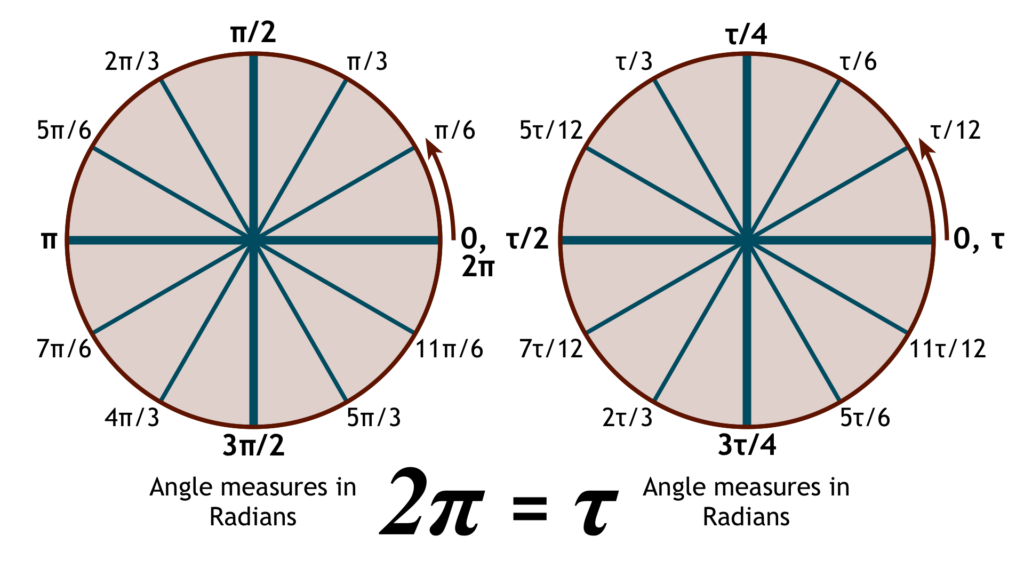
If you think modern mathematics is static and unchanging, you are very wrong. A prime example of this is the Tau movement — modern mathematicians who believe Pi is wrong. Now, nobody is arguing that C/d = π, as shown in the first diagram. However, Pi can be a bit of a handful when doing Trigonometry (sine and cosine functions, for example) with Radians, with 2π being the slightly arbitrary full cycle of a circle. Tau, roughly 6.28318, would be equal to 2π and define the full cycle of a circle in radians. Tau is equal to a circle’s Circumference (C) divided by its radius (r), instead of C/d.
This is gaining traction, however Pi is still used as standard. One of the challenges Tau faces is that Pi is more useful for day-to-day calculations using circles, while those who use radians on a regular basis would find Tau far more useful, however the debate remains interesting. What do you think?
Pi Day
Pi Day, also known as International Mathematics Day, is the most famous holiday in mathematics. It is celebrated on 14 March, as in the date format used by the United States, Canada and Belize, 14 March is represented by 3/14/YYYY which looks quite a bit like Pi!
An alternative celebration of Pi is Pi Approximation Day, celebrated on 22 July. One of Pi’s most accurate approximations used a lot in early mathematics is 22/7, so it is an alternative celebration for countries using the dd/mm/yyyy date format, as there is no fourteenth month. It is marked in a similar fashion to the more popular Pi Day.
This holiday was first celebrated in 1988, in an event held by a physicist at the San Francisco Exploratorium, which involved the consumption of fruit pies. Pi day aims to raise awareness about the importance of mathematics and its role in shaping our world, as well as to promote the beauty and relevance of mathematics to a wider audience.
The alternative to Pi, Tau, also has its own holiday. Tau Day is celebrated on 28 June by mathematicians who prefer Tau to Pi, and use the day to promote the use of the alternative constant. However, it is less well known than Pi or Pi Approximation Day.

The day is often celebrated by outreach events and the eating of pies, often decorated with a Pi symbol and the first few digits of Pi. It can also be marked by playing mathematical card games and maths jokes.
As an interesting coincidence, Albert Einstein was born on 14 March, the day which became Pi Day. The famous German-born theoretical physicist is widely held to be one of the greatest and most influential scientists of all time.

Is Pi actually the most important constant in mathematics?
Although many mathematicians might prefer Tau as the circle constant to Pi, or find Euler’s number, e, or the imaginary unit, i, more important for their particular area of maths, it would be hard to argue against Pi’s central place in mathematics. We use it every day.
Only you can decide. But it would be impossible to deny the incredible impact this almost magical number has had on all mathematics.