Srinivasa Ramanujan
Srinivasa Ramanujan (1887–1920) was a self-taught genius, born in India struggling to make a life for himself in the city then called Madras. However, his employers soon notice his mathematical talents, and he starts to contact professors of mathematics by writing letters to them.

His life
Srinivasa Ramanujan was born in 1887 in India, in what is now Tamil Nadu. Before even turning 10, he had the highest scores for the local primary examinations. He was a child prodigy at age 11, and he was constantly working with 2 local college students who lived with the family. Eventually he exhausted their knowledge too, and he was given advanced mathematical books, like one on trigonometry. Ramanujan commonly left questions that did not interest him blank, only spending time attempting the ones that he enjoyed or was challenged by.
As an intuitive mathematical genius, Ramanujan’s discoveries have influenced several areas of mathematics, but he is probably most famous for his contributions to number theory and infinite series, among them fascinating formulas that can be used to calculate digits of Pi in unusual ways.
Personal life
Ramanujan married Janaki Ammal in 1909, who was 10 years old at the time. Although this may seem weird to us now, it was quite common at the time. Although they were legally married, they did not see each other that often, as Janaki stayed at home with her mum for 3 years, and lived with her for only 2 years before heading to England alone to research mathematics further.
Throughout Ramanujan’s life, he had many health problems. During WW1, he was diagnosed with Tuberculosis, and was kept in a hospital. This led to him attempting to commit suicide in 1917. He was later arrested by Scotland Yard for this, as attempting suicide was a crime at the time, but he was released after his colleagues intervened.
He returned to India in 1919, where he would stay until his death in 1920, at the age of 32. Originally people believed his cause of death was Tuberculosis, but a recent analysis of his medical records revealed that it was more likely that he had been suffering from Hepatic amoebiasis, which was common in Madras, throughout his life. His life was dramatised in the 2015 film The Man Who Knew Infinity.
Career
In 1903, Ramanujan lost his scholarship because he neglected all other subjects for mathematics. He continued to pursue his own independent research in mathematics, while often living on the brink of starvation and in poverty. He attempted to find employment in 1910, when he met one of the founders of the Indian Mathematical Society, who introduced him to mathematicians across the area, including the secretary of the society who gave him a sponsorship to continue his research. This allowed him to start living in proper conditions in the city of Madras, and to begin enquiring for a job in mathematics.
His work began to be published in the Indian Mathematical Society Journal, and his genius became renowned in the community, including his solution to the infinite radicals problem. He kept on publishing work that resulted in him publishing a full paper. In Spring 1913, his work began being presented to major British mathematicians, where some ridiculed his work for having certain “holes”. However, the British mathematician Godfrey Harold Hardy sent a letter back with keen interest in his theorems, and began to share Ramanujan’s theorems with his colleagues, who all responded with a similar interest in them.
Later, Ramanujan was encouraged to spend time at Cambridge. Ramanujan’s Brahman upbringing would be against leaving the country, which meant that he originally refused. However, a year later, his parent’s removed their objection and allowed him to travel to England, which he accepted.
He arrived in England in March 1914, where he spent nearly 5 years collaborating with Hardy and his colleagues. Together they published many advanced mathematics papers. Ramanujan was formally taught the areas of mathematics that his short time in education didn’t cover, and Hardy received Ramunjan’s help for the mathematically rigorous proofs that were necessary at the time.
He was awarded a Bachelor Of Arts By Research Degree in March 1916, and he joined the London Mathematical Society in December 1917. He formally became a fellow of the Royal society in 1918, and he was elected A Fellow of Trinity College in Cambridge, being the first Indian to ever achieve this.
Srinivasa Ramanujan is renowned for many of his accomplishments, including his work on Infinite Sequences, and his novel investigations into mathematics.
His accomplishments
Ramanujan Summation
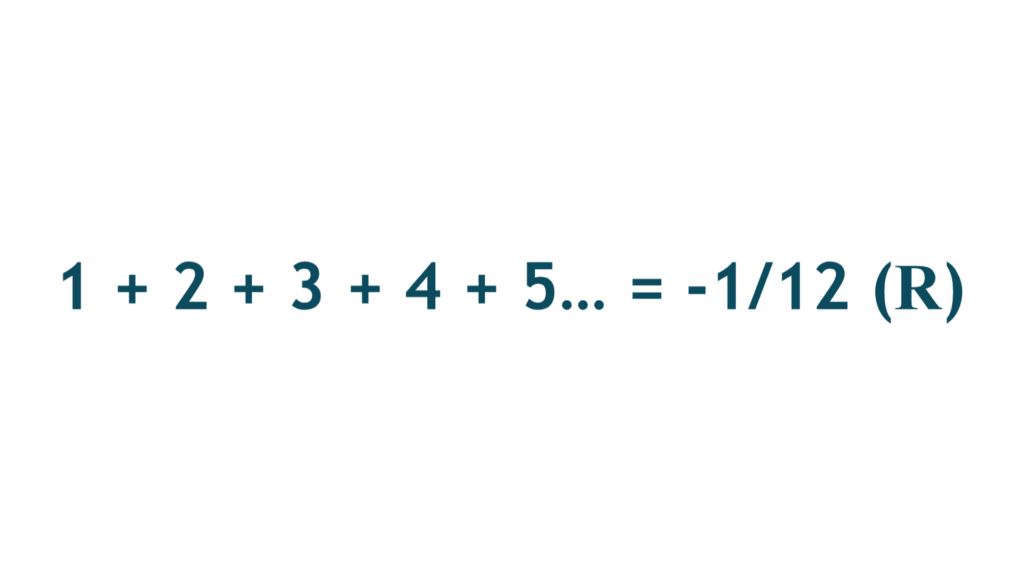
Ramanujan invented a novel way to “sum” divergent infinite series. Divergent series don’t have a sum in a traditional way, so Ramanujan created a different method of summation for these. This isn’t the traditional sum of the series, and it’s denoted with unique syntax to allow it to be clear that it is using Ramanujan Summation. When Ramanujan was looking at the infinite series: 1 – 1 + 1 – 1 + 1 – 1…, also known as the Grandi series, he determined that it has 2 clear values: 1 and 0. This, alongside multiple more advanced pieces of evidence, allowed him to state that the Grandi Series has a sum of 0.5 (R).
From this fundamental fact, Ramanujan was able to calculate the sum of multiple divergent infinite series, like the sum of all Natural Numbers. Although this technique may seem like a simple party trick, Ramanujan’s work on this can be applied to integrals, and can be used in advanced mathematics to provide plausible sums to compare the size of these complex sequences.
Ramanujan Primes
A Ramanujan Prime is a prime number that has a certain amount of primes (n) between itself, and half of itself, which satisfies another one of Ramanujan’s proofs; the prime counting theory.For example, 11 is a Ramanujan prime for (n=2) because between 5.5 and 11, there are 2 prime numbers: 7 and 11.
Ramanujan primes are useful to understanding the distribution of Prime Numbers. These can provide insight into prime numbers and the patterns between them.
Work on Number Theory
His work on Number Theory resulted in some of the most rigorous mathematical proofs of the time. These have been incredibly essential in modern mathematics.
Ramanujan’s work with Hardy resulted in a lot of these advanced theorems, and together, their Mathematical proofs have become essential to modern mathematics and science. For example, Ramanujan’s Master Theorem helps mathematicians solve complicated functions and integrals by changing their form. This is used in quantum mechanics to solve wave probability functions. This wasn’t even all of his work. Ramanujan’s work on number theory stretches from The Partition function, to Ramanujan’s Tau Function. These constantly appear in mathematics, and it’s thanks to the work of Ramanujan that this incredible world of mathematics has now been revealed.
The majority of these theorems are higher level proofs that you simply can’t do justice by describing. His work is one of the many mathematical wonders.
The Srinivasa Ramanujan Medal
Srinivasa Ramanujan was a renowned member of the Indian Mathematical Society, and his work was acknowledged in 1962, the Indian National Science Academy announced the Srinivasa Ramanujan Medal, awarded for work in the mathematical sciences. This award is handed out frequently, and honours Ramanujan for all of the work he has done.
Ramanujan’s work reminds all of us that you need a passion for mathematics, not a professional education or money, to become a great mathematician.