Quadratics
Ever tried to make the perfect basketball shot or wondered how satellite dishes are shaped just right? The secret lies in quadratic equations, a powerful tool in algebra that helps us understand how things curve, speed up, slow down, or reach a peak.
This article contains all of the knowledge and skills required for the GCSE Higher Mathematics exam.
Quadratics are introduced early in secondary school and continue to play an important role in fields like physics, engineering, economics, and computer science. At the core of it all are parabolas, the U-shaped graphs that represent quadratic equations and appear in everything from video games to business models. Quadratics are the first truly non-linear equations you meet in your mathematical journey. Instead of a boring straight-line, they curve, dip, and rise in elegant parabolas. In exams you’ll be asked to solve them by different methods, sketch their graphs, or use them in worded problems.
The word quadratic comes from the Latin word quadratus, meaning “square”
By the time students are 16, usually they should be able to:
- Solve quadratic equations by factorising, completing the square, or applying the quadratic formula.
- Sketch quadratic graphs by finding roots, y-intercepts, and turning points.
- Interpret the discriminant to discuss the number of solutions.
- Model problems with quadratic equations — areas, rectangles, speed–time graphs, and sequences.
Each skill targets the same object: the quadratic expression ax2 + bx + c.
What is a quadratic?
A quadratic equation is any equation written like this:
ax² + bx + c = 0
Where a, b, and c are constants (and a can’t be zero), and x is the variable. This is called a second-degree polynomial because the highest power of x is 2.
When you graph a quadratic equation, it forms a parabola:
Parabolas are perfectly symmetric, meaning that if you folded the graph in half along its axis of symmetry, both sides would match.
Satellite dishes, car headlights, and even water fountains trace parabolic paths.
Solving quadratic equations
To solve a quadratic equation means finding the x-values, called roots or solutions, that make the equation true, that is, the values where the graph crosses the x-axis.
These solutions can represent real-world things, like how long a ball stays in the air, when two vehicles cross paths, or what value a business breaks even at.
Each of the following methods shows where the curve hits the horizontal axis — those points often tell us when something starts, stops, or reaches a goal. Understanding the shape of the curve helps you figure out key moments in whatever situation you’re analysing.
A reminder: quadratics are written in the form ax2 + bx + c = 0.
Factoring
This involves splitting the equation into two parts that multiply to zero.
For example: x² + 5x + 6 = 0 becomes (x + 2)(x + 3) = 0 ∴ x = -2 or x = -3
The easiest way to factorise quadratics where a = 1 is to work out the two numbers that add to b and multiply to c. These are the numbers added to x in the factorised terms from which the roots can be found.
As the quadratic has been factorised into two terms multiplied against one another, if the solution of either or both of the terms is 0, then the solution will be zero. Values of x that make the solution zero are the x-intercepts, the roots, of the quadratic.
On a trickier paper, you’ll also see harder questions where a does not equal 1.
For example: 2x2 + 7x + 6 = 0 becomes 2x2 + 4x + 3x + 6 = 0 ∴ 2x(x + 2) + 3(x + 2) = 0 ∴ (2x + 3)(x + 2) ∴ x = -3/2 or x = -2
This method is called splitting the middle term. An alternative is using the ‘grid method’:
| x | + 2 | |
| 2x | 2x2 | + 4x |
| + 3 | + 3x | + 6 |
This method involves writing the quadratic in a 2×2 table, also with its middle term split. Then, at the front of each row and column, write the HCF (Highest Common Factor) of the terms in that row or column. The sum of the tops of the columns and the sum of the fronts of the rows produce the two factorised terms that are multiplied against each other.
Again, as the quadratic has been factorised into two terms multiplied against one another, if the solution of either or both of the terms is 0, then the solution will be zero. Values of x that make the solution zero are the x-intercepts, the roots, of the quadratic.
If a quadratic doesn’t factorise nicely, don’t panic! If you are doing a non-calculator paper, you are probably wrong and need to try again, and if you are doing a calculator paper, just use the quadratic formula!
Completing the square
This involves rearranging the equation into a perfect square. You may be asked to write a quadratic in the form (x + p)2 + q.
For example: x² + 6x + 5 becomes (x + 3)² – 4 = 0 ∴ x = -1
These are pretty simple and here’s what you do (again, other variations are available):
- Halve the coefficient of x: 6/2 = 3.
- Square it: 9
- ∴ x2 + 6x + 5 = (x + 3)2 – 4
From this form, you can instantly read off the vertex (–3, –4). This skill links directly to graph-sketching questions: examiners want you to show the vertex without drawing the whole parabola.
Using the quadratic formula
The quadratic formula is reliable and works for every quadratic:
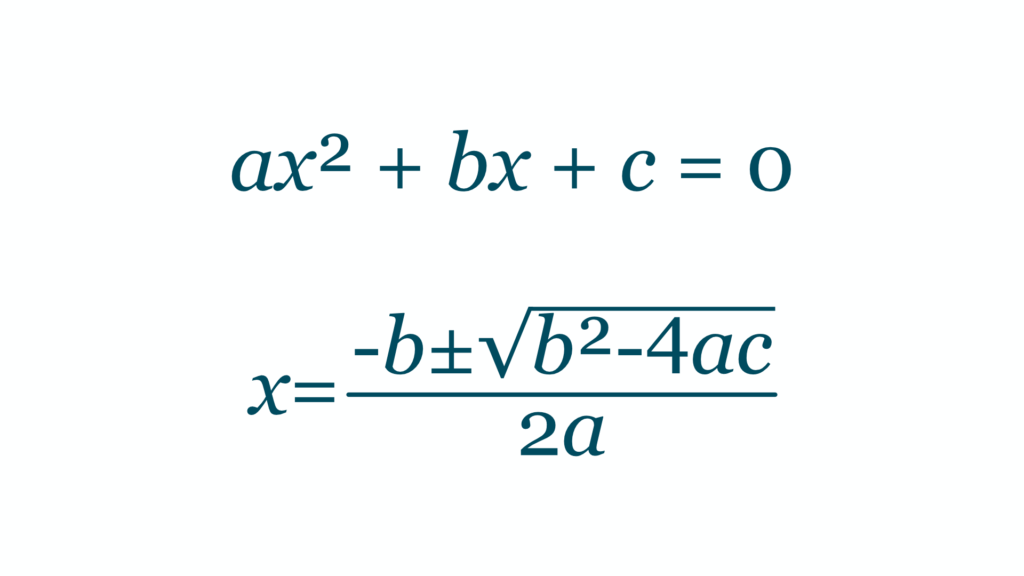
Sometimes factorising just won’t work nicely, for example: 2x2 – 4x – 7 = 0.
This is where examiners expect you to confidently apply the quadratic formula.
In mark schemes, full credit comes only if you substitute correctly: a = 2, b = -4, c = -7. For many students, the substitution and simple arithmetic orchestrate their downfall not the actual quadratic!
The quadratic formula originates from Muhammad ibn Musa al-Khwarizmi’s 9th-century text on “completing the square.”
The discriminant
The discriminant, the part under the square root in the quadratic formula (b2 – 4ac), tells you how many real solutions an equation has. If it’s greater than zero, it has two real solutions. If it equals zero, it has one real solution. If it’s less than zero it has no real solutions, but two complex ones.
You may be explicitly tested on whether you know that b2 – 4ac tells you the number of solutions.
For example: Show that the quadratic kx2 + 4x + 1 = 0 has no real solutions for certain values of k.
Here, you must argue determinedly that if b2 – 4ac < 0, then no roots exist. This is a part of specs that is often forgotten, and can provide some straightforward marks provided you know it.
Quadratics in context
Your exam may also have a modelling twist or two, with questions like:
- Geometry: “The length of a rectangle is 3 more than its width. Its area is 54 cm². Form a quadratic and solve.”
- Sequences: “A quadratic sequence has nth term an^2+bn+c. Given the first three terms, find a, b, c.”
- Kinematics: “A ball is thrown upwards with speed 8 m/s. Its height after t seconds is h = 8t – 5t2. Find when it hits the ground.”
These questions test whether you can set up and solve quadratics in unfamiliar settings and often converge with physics!
From Babylonian clay tablets to Persian algebra, quadratics have a long history. Al-Khwarizmi’s work in Baghdad (c. 820 AD) created a systematic method for solving quadratics, centuries before symbolic algebra existed. Later, renaissance mathematicians refined the general formula. Today, every maths student retraces their steps!
Key features of a parabola

- Vertex: The highest or lowest point (depending on the direction of the curve)
- Axis of Symmetry: The vertical line that cuts the parabola in half, Formula: x = -b divided by 2a
- Roots or Solutions: The points where the curve crosses the x-axis (y = 0)
- Y-Intercept: Where the parabola crosses the y-axis (when x = 0); this is equal to c
The vertex is often key in real life, it might tell you the maximum height of a rocket, the minimum cost of a product, or the best angle to launch something at.
Graphing quadratic equations
These questions involve sketching the quadratic on a graph having worked out its roots, y-intercept and vertex.
For example: Sketch y = x2 – 4x + 3
To do this you would:
- Factorise to find roots → x = 1 and x = 3 (x2 – 4x + 3 becomes (x – 1)(x – 3) = 0 ∴ x = 1 or x = 3)
- y-intercept → (0,3)
- Vertex → complete the square: (x-2)2 – 1
The examiner expects you to mark these features – there’s no need for perfect symmetry, but the key points must be labelled to avoid confusion, or to stifle the common examiner’s argument that ‘points are unclear’.
Why quadratics matter
Quadratics aren’t just for maths exams, they’re all around us. In physics, they model falling objects, projectiles, or acceleration. Engineering uses them to design bridges, parabolic mirrors, or reflector dishes. In business and economics, quadratics are used to find the most profitable points or the lowest costs. Quadratics are used in computer graphics for smooth animation, curved motion, and collision detection. They are also used in video games to simulate jumps, gravity, and arcs.
From engineering challenges to everyday problems, quadratics help us make predictions, optimise designs, and understand the world in motion. Whether you’re solving equations for homework or designing the next game physics engine, understanding how parabolas work is both practical and exciting.
Quadratics are more than a checklist, they’re a test of versatility. Can you switch from factorising to completing the square to the formula? Can you sketch confidently? Can you translate a word problem into an equation? Master these, and you’re not just exam ready — you’ve taken your first steps into the algebra that powers physics, engineering, and beyond.