Real Numbers. Sounds a bit simple does it not? Well, actually, there is an impressive ‘Russian doll’ of types of numbers, that we have encountered as we learn more about mathematics. So, want to find out what they are?
Classifying Numbers
If you think of a number, you will probably think of a Real Number. Just to clarify, there are some actual numbers that are not ‘Real Numbers’. That is just the confusing way mathematicians seem to name their terms.
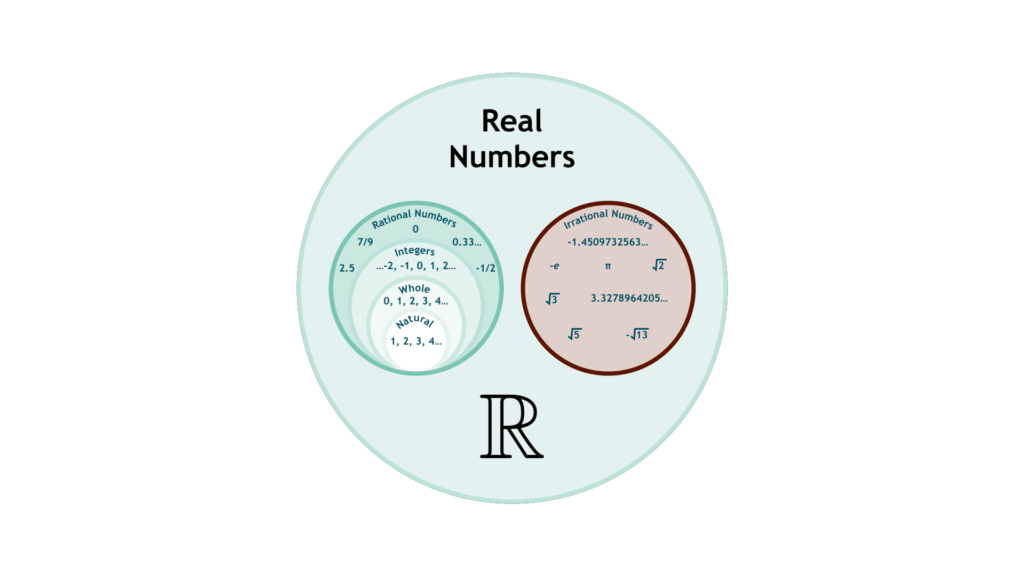
So you might have thought of 2π, -4.5, 5.77 recurring, √2, 0, 12, 6/7 or e. They are all Real Numbers. A Real Number, represented by an ‘ℝ’ symbol, is a number that can be used to measure a ‘continuous one-dimensional quantity’. These could include distance, duration and temperature. In language easier to understand, this means that a Real Number is a number that can be represented on a number line; either 0, a negative number or a positive number. They can all be represented by almost unique finite decimal expansions.
You might notice that this quaint setup of mathematical Russian Dolls corresponds to the development of human understanding of maths. We have been aware of Natural Numbers since the dawn of civilisation, due to the need for basic counting, while the invention of 0 is relatively recent, from around 2,000 years ago. The number first appeared in Mesopotamia, (modern-day Iraq) around 3 BCE, with the Mayans making an independent discovery about 7 years later. These ideas soon spread across the world. It is believed the Indian Brahmagupta discovered integers in the 7th century. The expansion into Rational, Irrational and Real numbers is slightly patchier, however it is believed that Complex Numbers were discovered in 16th century Italy.
There are two types of Real Numbers: Rational Numbers (ℚ) and Irrational Numbers (I). A Rational number can be defined by the quotient, or fraction, of two integers where the denominator is not 0. So basically, any fraction, decimal that does not go on forever or a basic integer, 0, positive or negative. However, recurring decimals are still Rational Numbers, as for example, 0.33… can be represented as 1/3.
The most basic type of number is a Natural Number (ℕ). This set includes basic numbers from 1 upwards. 1, 2, 3, 4, 5… all the way upwards. Whole Numbers (W) introduce the number 0, but are otherwise the same. Integers (ℤ) add negative numbers to their field. The Rational Numbers also include finite or recurring decimals and fractions. Irrational Numbers (I) are Real Numbers that cannot be represented by a quotient. The most famous examples of Irrational Numbers include π, e, φ (the Golden Ratio) and √2. Any positive or negative square root that isn’t perfect (equal to an integer) is irrational, and any number defined by infinite decimal expansion, in other words going on forever.
So what numbers are not Real? Well, an Imaginary Number is not real. They are called imaginary numbers, as when they were originally conceived they were considered a joke, however people researched them more and discovered they were actually useful and important because they filled a gap in mathematics, but the “imaginary” name has stuck. The “imaginary” number i has the property that the square of i is -1. It is a rather curious fact that ii is actually a real number!
An Imaginary Number is a Real Number multiplied by the imaginary unit ‘i’, where i^2=-1. The combination of a Real Number by itself and an Imaginary Number is a Complex Number, the most advanced kind of number. These can be plotted on the Complex plane, a special plane where Real (Re) is plotted against Imaginary (Im), which can be used to help solve problems, like quadratic equations, that do not have Real solutions.
Between every two rationals, there is an irrational. Between every two
irrationals, there is a rational. Nevertheless, there are infinitely more irrationals
than rationals, of which there are only a countable number.
You might be wondering what the point of all of this is. For the same reason we classify anything, we want to make sure that everyone has an understanding of what specific numbers are called and what they mean. After all, there’s a difference between 25, and -32, and 46. And if you want to or have studied maths until calculus, these symbols are very useful in defining the parameters of mathematical laws. There are also applications in set theory, logic and physics.
A quick quiz
1) √121
Is the number above rational or irrational?
A) Rational
B) Irrational
2) √32
Is the number above rational or irrational?
A) Rational
B) Irrational
3) -13/12
Is the number above rational or irrational?
A) Rational
B) Irrational
4) √99
Is the number above rational or irrational?
A) Rational
B) Irrational
5) -0.32
Is the number above rational or irrational?
A) Rational
B) Irrational
6) √28
Is the number above rational or irrational?
A) Rational
B) Irrational
7) 0.5555
Is the number above rational or irrational?
A) Rational
B) Irrational
Answers
1) A a perfect square — equivalent to 11 2) B not a perfect square 3) A a ratio of two integers 4) B not a perfect square 5) A a ratio of two integers —equivalent to -32/99 6) B not a perfect square 7) A a ratio of two integers — equivalent to 5555/10000