You may not have heard of Hyperoperations, but you probably use it every day. Read on to explore past the basic Hyperoperations sequence, and discover Tetration and Pentation!
The Hyperoperation sequence is an infinite sequence of operations, with the next in the sequence allowing for larger numbers to be made. Simple operations like addition, multiplication, and exponents are the first elements in this sequence, but it continues!
Meet Tetration, also known as Hyper-4. Similar to how multiplication is repeated addition, or exponents are repeated multiplication, tetration is repeated exponentiation.
To understand tetration, you first need to understand the basic concept that underlies it. In the more common Rudy Rucker Notation, tetration is written in the format nx where n refers to the number of ‘floors’ used in the exponent.
A basic exponent, like 22 is 2 floors high. So, an exponent like 22^2, has 3 floors.
To solve these exponents, you should work from the highest 2 floors down. So, if you wanted to do 22^2 first you solve 22 and then 24, solving from the inside outwards.
There is one key point with Tetration notation. Every floor must have x as the power, or else it can’t be expressed as Tetration, and would instead use basic exponential notation.
You might have noticed a key reason you don’t hear about tetration very often. Using it creates large numbers very quickly… 310 is 1 with 10 billion zeros, which is larger than the number of atoms in the observable universe. If anyone wanted to write this number on an infinite supply of paper, they would be dead before they could finish it.
If Tetration is repeated exponentiation, then is it possible for there to be repeated Tetration? The answer is yes. The next step is Pentation, Hyper-5, tetration’s big brother.
Pentation is written in multiple formats, and there isn’t a common standardised one like for tetration, instead we’ll use the most simple format, which looks similar to tetration.
[2 pentated 3 times] is an example of a number in this format. It might not look that complex, but this number has 3 floors of tetration, which looks like this 2^22
This might seem simple, but it isn’t: the solution is 65,536!
One of the earliest mentions of hyperoperations was that of Albert Bennett in 1914, in which he developed part of his theory of commutative hyperoperations. Twelve years later, Wilhelm Ackermann defined ‘ϕ,’ a function like a sequence of hyperoperations. In a 1947 paper, the Greek Ruben Goodstein introduced a sequence of operations now called hyperoperations, and extended operations beyond exponentiation, adding the next steps, suggesting they be called tetration and pentation. As a function with three arguments, it is seen to be a version of the original Ackermann function.
So can pentation be repeated? Of course it can! Hexation is the start of the more complex areas in the Hyperoperation sequence and can’t be written in a simple format like Tetration or Pentation. It is, put simply, repeated Pentation and doesn’t have many real-world use cases.
In Theory, the hyperoperation sequence can continuously recur, and would instead begin to use a formula and formal calculations to solve, instead of the simple “floor” concept and simpler notation from before. The formula for this is shown on below, but doesn’t account for addition. n represents the operation being conducted. For multiplication, n=2, for exponentiation, n=3, for Tetration, n=4, and for Pentation n=5, etc.
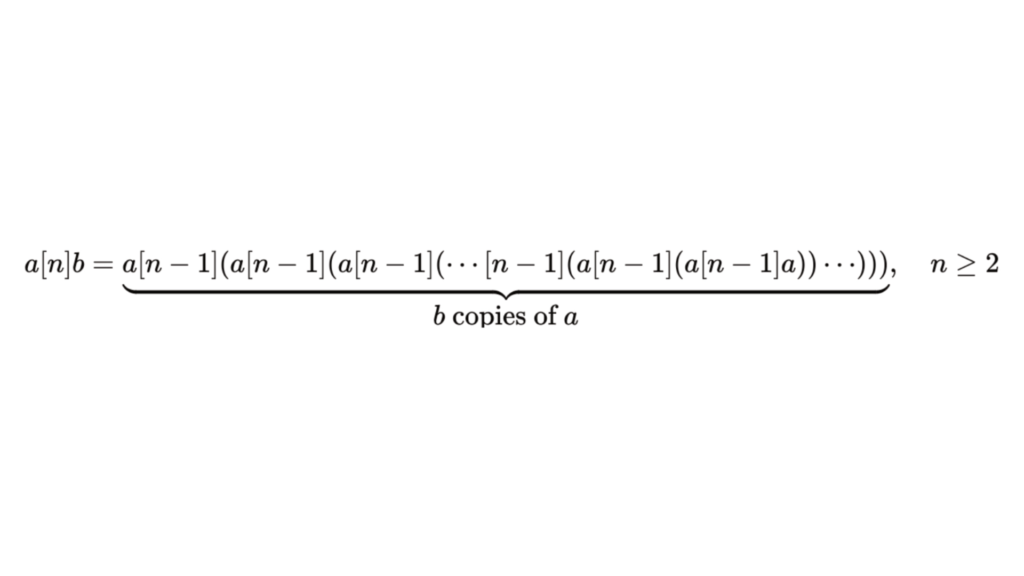
So why are these Hyperoperations useful? Some functions and concepts can be extended using hyperoperation. They are essential to large numbers comprehension. New larger infinities and their properties arise using its ideal notion and class notion, and derivative and integral concepts from calculus are also extended with hyperoperations.
To summarise, Hyperoperations are a complex and fascinating sequence, showing how much maths lies beyond the day-to-day operations we use.