Pythagoras’ Theorem
Likely the most renowned theorem in the geometric world, many consider Pythagoras’ famous theorem to be the most important one too. A catalyst for the discovery of irrational numbers, the subject of so many proofs, possibly the most widely-known mathematical theorem in the world, this is the Pythagorean Theorem.
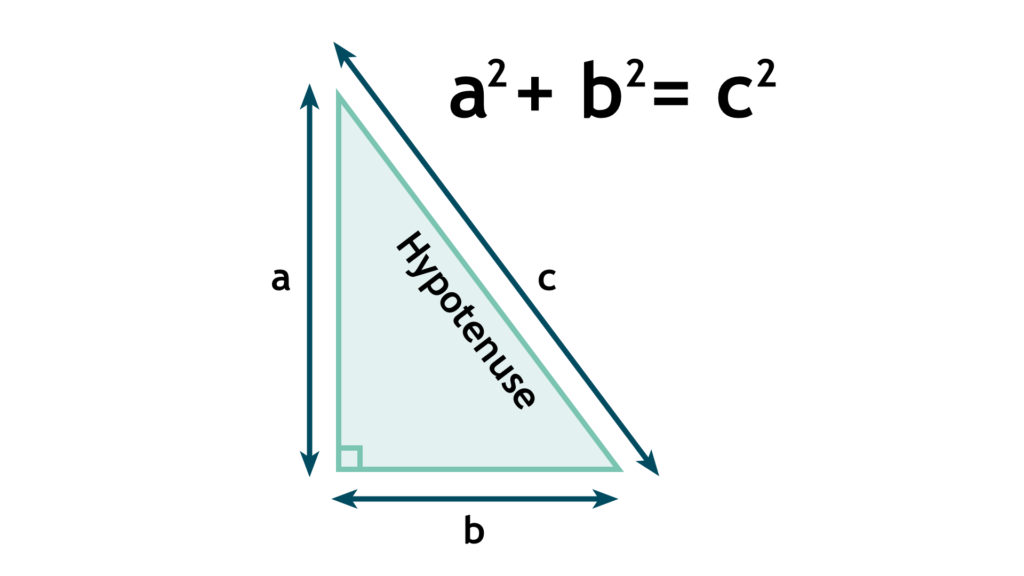
The Pythagorean Theorem is likely the most renowned theorem in the geometric world, and many consider it the most important one too. The theorem states that in a right-angled triangle, the sum of the squares of the two perpendicular sides, is the square of the length of the diagonal side, also known as the hypotenuse.
When expressed algebraically, we end up with the statement a2 + b2 = c2.
A right-angled triangle that has a length of 1 for the perpendicular sides is what led the ancient Greeks to believe in irrational numbers. The pythagorean theorem states that a2 + b2 = c2. However, 12 + 12 = 2, which means that the length of the hypotenuse to be √2, which is in irrational number that begins with 1.4142 and goes on endlessly. This really annoyed Pythagoras’s followers, who wanted to keep these irrational numbers a secret. When one of them kept talking about it, they were thrown off a cliff.
Why is this theorem so important in modern mathematics?
The Pythagorean Theorem was relevant for many people in Ancient Greece as it led to belief in irrational numbers, which are a fundamental type of real number, that can’t be expressed as simple integer ratios. Not only this, but the Pythagorean Theorem is incredibly simple and straight forward. Everybody learns it, and, hopefully, everybody memorises it!
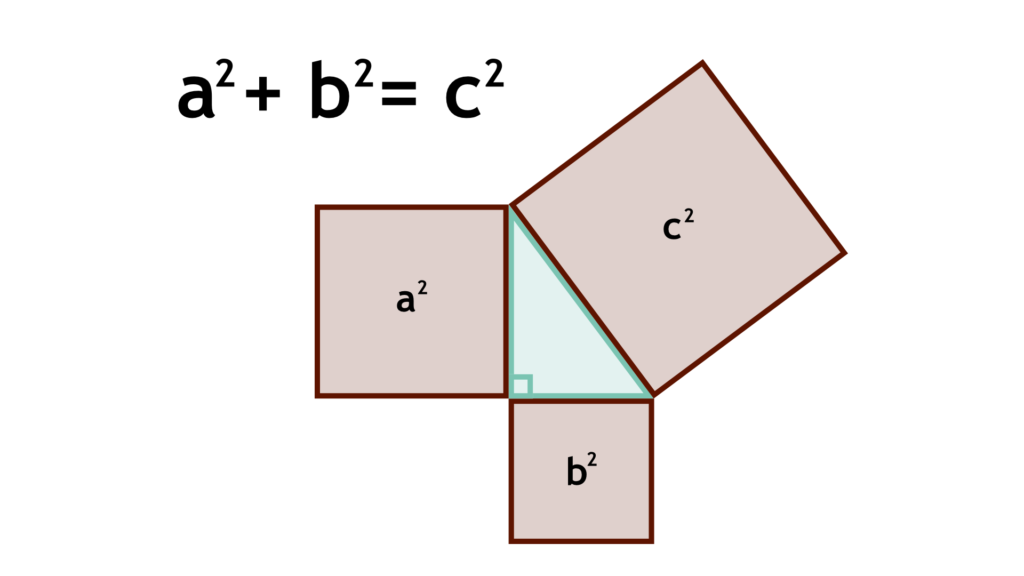
The Pythagorean Theorem also distinguished the Euclidean Geometry that we all know well from the Non-Curved Non-Euclidean Geometry by identifying that a right-angled triangle drawn on a sphere wont follow the theorem.
How is it used in daily life?
A common question in mathematics is “will I ever end up using this?” and the answer generally ends up being yes. Whether you become a mathematician or follow a different career path, it is very likely that you will be using the Pythagorean theorem regularly.
The Pythagorean Theorem is a fundamental principle in geometry that is heavily used in many careers, like Architecture. It is always faster to travel along the Hypotenuse than travel along both of the other edges. This leads to the pythagorean theorem becoming essential in other careers such as Geography, where it is frequently used by map designers and surveyors, and even astronomers use it to calculate the distance between stars and galaxies in the universe. Computer Graphics Designers and pilots also use it daily to calculate distances and angles.
How did the Greeks prove this?
It’s believed that Pythagoras himself came up with some of the proofs popularly shown today.
Although the discovery of the Theorem is widely credited to Pythagoras, it is debated among historians whether the theorem was discovered at many places at different times, and when the first discovery and proof truly were.
A fascinating aspect about the Pythagorean Theorem is that it is far more than just fact. New proofs for the Pythagorean Theorem are constantly being discovered, adding a unique total that exceeds 400. Recently, a group of schoolchildren discovered a sensational new proof using trigonometry — an impressive feat given most of trigonometry relies on the theorem itself. Here are two popular proofs of the theorem:
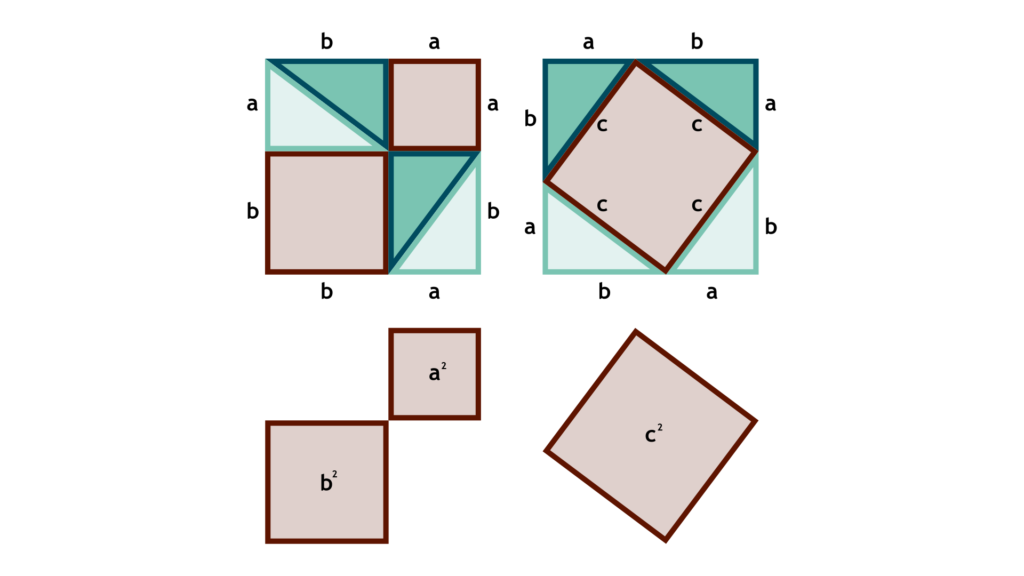
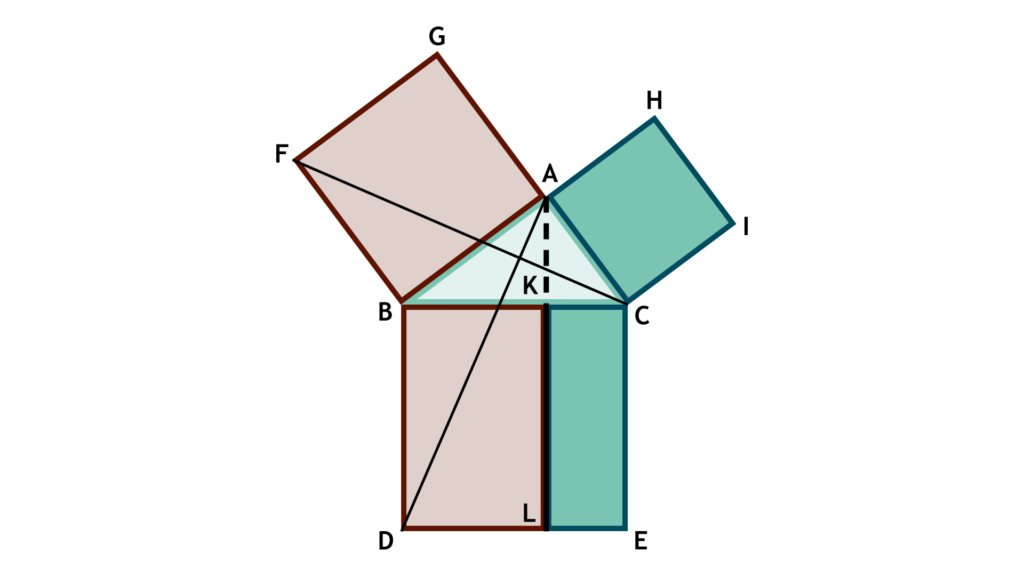
The Pythagorean Theorem is more than just a theorem
The Pythagorean Theorem is far more than just a simple equation. Many regard it at a statement of mathematical beauty, and pythagoras himself believed strongly that the universe was interconnected through maths, music and harmony. The theorem is widely used to represent balance. It has been used in literature throughout time, from Plato’s book “The Republic” where it is used as an expression to society’s balance, to a reference for Moby Dick’s quest for truth and knowledge.
Pythagorean Triples are 3 numbers, where the two of them squared will sum to the square of the other. This means that they can be a perfect right-angled triangle. The most commonly known example of this is 3 4 5, however there are 16 that contain numbers less than 100. Pythagorean triples are often regarded to be a sign of natural beauty, and they can be found in modern mathematics and science.
If a Pythagorean Triple is primitive, it means that all three digits are coprime. This means that by finding one triple, you can multiply by a set factor to find infinitely more, like 6 8 10 or 9 12 15 from 3 4 5.
Did the Pythagorean Theorem change mathematics?
Although many mathematicians might state other, more important mathematical events that influenced the history of maths, like the discovery of logarithms or the defining of Trigonometric ratios, it is truly undeniable that the Pythagorean Theorem shaped modern mathematics.
During his time as a philosopher, Pythagoras identified the “root of reality” in what he called the “tetracyts”. This consists of the first 4 integers – 1,2,3,4, which when added together create 10, which Pythagoras believed to be the perfect number.
Many people commonly believe that the Pythagorean Theorem is far too simple for it to be significant, however this makes it something that anybody can understand to admire the true beauty of mathematics and nature.