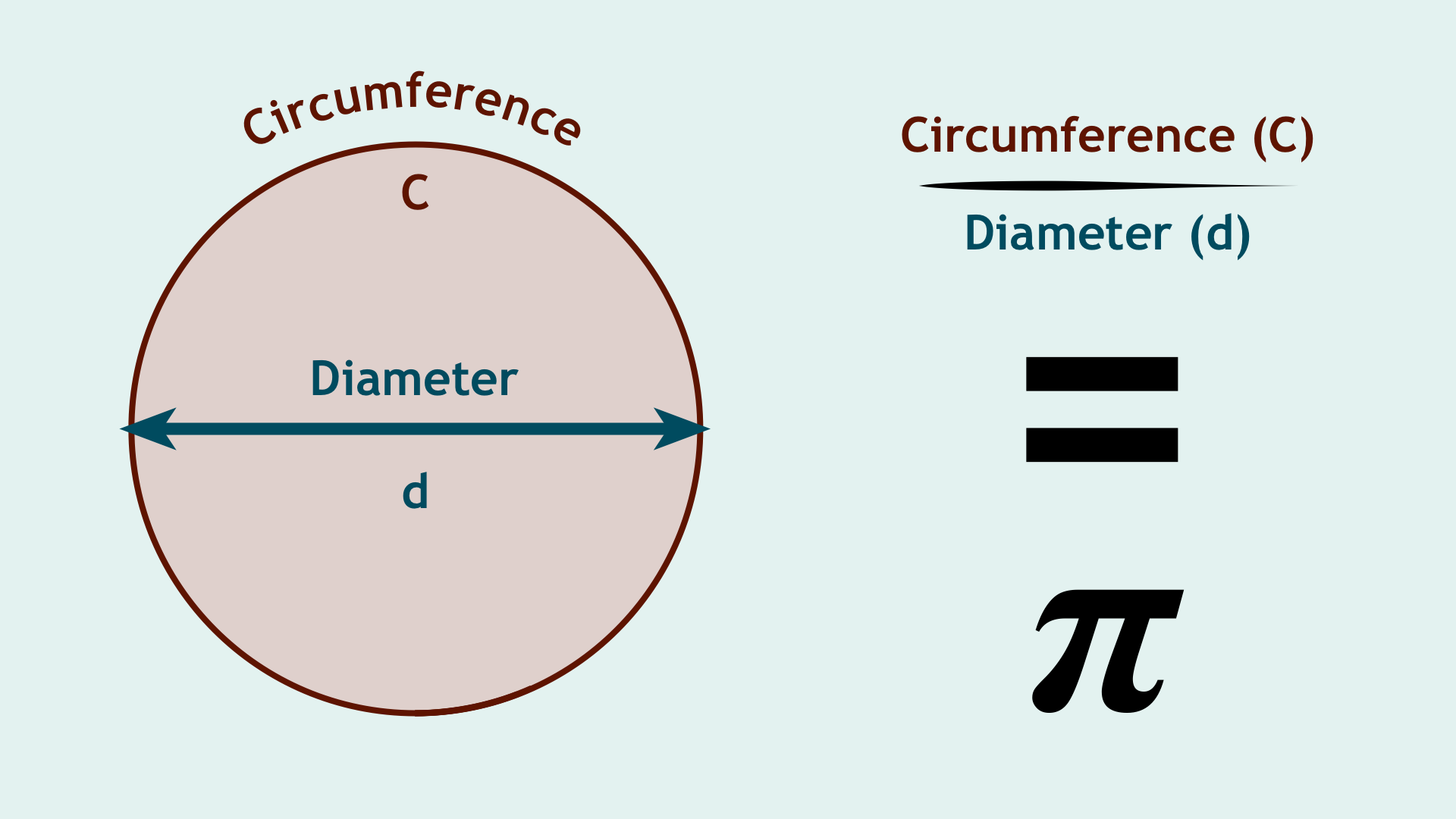
At its heart, Pi can be defined as the ratio between the circumference and diameter of a circle, which is always the same. Pi is defined by an infinite decimal expansion, meaning that it has an infinite number of digits, and cannot be expressed exactly as a ratio. This makes it an irrational number, as discovered by Johann Heinrich Lambert in 1761, that we can only approximate, which is why in equations it is represented by the symbol π. Pi is also transcendental, meaning that Pi is not the root of any algebraic equation with rational coefficients. It even has its own holiday!
Why Pi? The letter π is the first letter in the Greek word for “periphery”, the “periphery” of a circle being the precursor to the “perimeter” of a circle, which today we call a circle’s circumference. British mathematician William Jones chose the Greek letter as the constant’s symbol in 1706, but it was mostly popularised by Leonhard Euler.
Estimating Pi — an ancient mathematical curiosity
Despite having been known about for millennia, the earliest deduction of Pi recorded was found on the famous Egyptian Rhind Papyrus, written in around 2,000 BCE. The value it showed was 3.16045, a surprisingly accurate estimate, however the Babylonians were actually more accurate, as shown on tablets. The incredible mathematician Archimedes of Syracuse was the first person to calculate Pi, using his Pythagorean Theorem to approximate it using polygons. Around 2,500 years later, a brilliant Chinese mathematician and astronomer Zu Chongzi introduced the approximation 355/113. This is correct to six decimal places.
Pi is actually a part of Egyptian mythology. People in Egypt believed that the pyramids of Giza were built on the principles of pi. The vertical height of the pyramids have the same relationship with the perimeter of their base as the relationship between a circle’s radius and its circumference. The pyramids are phenomenal structures and are one of the seven wonders of the world.
The Indian mathematician Srinivasa Ramanujan established several formulae for calculating Pi, like many other famous mathematicians. One of these correctly predicted Pi to 8 decimal places. Euler also worked successfully on a formula for Pi, but he now has his own famous mathematical constant!
The calculation of pi is a stress test for a computer. It works just like a digital cardiogram since it indicates the level of activity within the computer’s processor.
Computers revolutionised the accuracy with which we could predict Pi. In 1948, D.F. Ferguson and John W. Wrench achieved a result correct to 808 places. In December 2002, 10 mathematicians led by Professor Yasumada Kanada took more than a hundred hours of computer time to calculate the value of Pi correctly to an incredible 1.24 trillion digits.
3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679
Pi to 100 digits
Why is Pi useful?
The constant π helps us understand our universe with greater clarity. The definition of π inspired a new notion of the measurement of angles, a new unit of measurement. These radian measurements have been important in giving rise to many important insights in our physical world.
Trigonometric functions, which in the real world are crucial for navigation, triangulating locations and working out precise distances, rely on angles. In Radians, the choice angle measurement for Trigonometry, Pi is used to measure angles, with a complete circle span of 2π equalling 360°. Pi is also used in calculus to calculate integrals and derivatives, and has even been found cropping up in physics recently.
It is claimed that Pi even describes the bendiness of rivers. You can measure how “bendy” a river is by measuring its total length and dividing by straight route from its source to mouth, this measure is called “sinuosity”. So a totally straight river would have a sinuosity of 1, while very bendy rivers can have very high sinuosity, with no limit to how high it can go. Yet, it is claimed the average sinuosity of rivers around the world is Pi. This is an incredible fact, and if true means that rivers are typically a little over three times longer than the direct route from source to mouth. Of course some rivers are straighter, and some rivers are longer, but the average sinuosity is around 3.14.
In its more simple use cases, Pi allows you to find the circumference or area of circle using πr2 and πr2 respectively. This is crucial for basic construction and calculation. On a solid level, Pi is also used to calculate the surface areas and volumes of cylinders and cones. You can find out more in our Guide to Shapes and Solids.
So, it is a good bet you have encountered Pi very often in your life — even if you don’t realise it!
Is Pi actually wrong?

If you think modern mathematics is static and unchanging, you are very wrong. A prime example of this is the Tau movement — modern mathematicians who believe Pi is wrong. Now, nobody is arguing that C/d = π, as shown in the first diagram. However, Pi can be a bit of a handful when doing Trigonometry (sine and cosine functions, for example) with Radians, with 2π being the slightly arbitrary full cycle of a circle. Tau, roughly 6.28318, would be equal to 2π and define the full cycle of a circle in radians. Tau is equal to a circle’s Circumference (C) divided by its radius (r), instead of C/d.
This is gaining traction, however Pi is still used as standard. One of the challenges Tau faces is that Pi is more useful for day-to-day calculations using circles, while those who use radians on a regular basis would find Tau far more useful, however the debate remains interesting. What do you think?
Pi Day
Pi Day, also known as International Mathematics Day, is the most famous holiday in mathematics. It is celebrated on 14 March, as in the date format used by the United States, Canada and Belize, 14 March is represented by 3/14/YYYY which looks quite a bit like Pi!
An alternative celebration of Pi is Pi Approximation Day, celebrated on 22 July. One of Pi’s most accurate approximations used a lot in early mathematics is 22/7, so it is an alternative celebration for countries using the dd/mm/yyyy date format, as there is no fourteenth month. It is marked in a similar fashion to the more popular Pi Day.
This holiday was first celebrated in 1988, in an event held by a physicist at the San Francisco Exploratorium, which involved the consumption of fruit pies. Pi day aims to raise awareness about the importance of mathematics and its role in shaping our world, as well as to promote the beauty and relevance of mathematics to a wider audience.
The alternative to Pi, Tau, also has its own holiday. Tau Day is celebrated on 28 June by mathematicians who prefer Tau to Pi, and use the day to promote the use of the alternative constant. However, it is less well known than Pi or Pi Approximation Day.

The day is often celebrated by outreach events and the eating of pies, often decorated with a Pi symbol and the first few digits of Pi. It can also be marked by playing mathematical card games and maths jokes.
As an interesting coincidence, Albert Einstein was born on 14 March, the day which became Pi Day. The famous German-born theoretical physicist is widely held to be one of the greatest and most influential scientists of all time.

Is Pi actually the most important constant in mathematics?
Although many mathematicians might prefer Tau as the circle constant to Pi, or find e or the Golden Ratio more important for their particular area of maths, it would be hard to argue that Pi is not the most important constant in mathematics.
While e is useful in analytics and the Golden Ratio in nature, Pi can be used on a day-to-day basis to calculate the areas and circumferences of circles, and by extension further geometric problems.
However, only you can decide. But it would be impossible to deny the incredible impact this almost magical number has had on all mathematics.
By K Gan and C Cooper